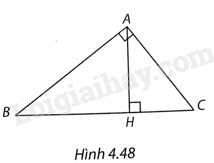
Giải bài 8 trang 95 vở thực hành Toán 9Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết (AH = 4,CH = 3) (H.4.48). a) Giải tam giác ABC (Góc làm tròn đến độ, cạnh làm tròn đến chữ số thập phân thứ nhất). b) Giải tam giác ABH (Góc làm tròn đến độ, cạnh làm tròn đến chữ số thập phân thứ nhất). c) Tính giá trị biểu thức (M = frac{{sin B + 3cos B}}{{cos B}}). Đề bài Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết \(AH = 4,CH = 3\) (H.4.48).
a) Giải tam giác ABC (Góc làm tròn đến độ, cạnh làm tròn đến chữ số thập phân thứ nhất). b) Giải tam giác ABH (Góc làm tròn đến độ, cạnh làm tròn đến chữ số thập phân thứ nhất). c) Tính giá trị biểu thức \(M = \frac{{\sin B + 3\cos B}}{{\cos B}}\). Phương pháp giải - Xem chi tiết a, b) Trong một tam giác vuông, nếu cho biết trước hai cạnh (hoặc một góc nhọn và một cạnh) thì ta sẽ tìm được tất cả các cạnh và góc còn lại của tam giác vuông đó. Bài toán này gọi là bài toán Giải tam giác vuông. c) Thay \({\widehat B^o} = {37^o}\) vào M, ta tính được M. Lời giải chi tiết a) Trong tam giác vuông AHC vuông tại H, theo định lí Pythagore, ta có \(A{C^2} = A{H^2} + H{C^2} = {4^2} + {3^2} = 25\) nên \(AC = 5\) \(\tan C = \frac{{AH}}{{HC}} = \frac{4}{3}\), suy ra \(\widehat C \approx {53^o}\) Tam giác ABC vuông ở A nên ta có \(\widehat B = {90^o} - \widehat C = {90^o} - {53^o} = {37^o}\) \(\tan C = \frac{{AB}}{{AC}}\) nên \(AB = AC.\tan C = 5.\tan {53^o} \approx 6,6\) Theo định lí Pythagore, ta có \(B{C^2} = A{B^2} + A{C^2} = {5^2} + {6,6^2} = 68,56\) nên \(BC \approx 8,3\) b) Tam giác ABH có vuông tại H, theo định lí Pythagore, ta có \(B{H^2} = A{B^2} - A{H^2} = {6,6^2} - {4^2} = 27,56\) nên \(BH \approx 5,2\) \(\sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{{5,2}}{{6,6}}\) nên \(\widehat {BAH} \approx {52^o}\) c) Ta có: \(M = \frac{{\sin B + 3\cos B}}{{\cos B}} = \frac{{\sin {{37}^o}}}{{\cos {{37}^o}}} + 3 = 0,8 + 3 = 3,8\)
|