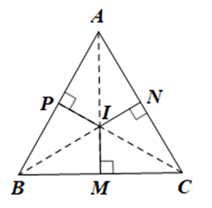
Giải Bài 87 trang 94 sách bài tập toán 7 - Cánh diềuCho tam giác đều ABC có I là điểm cách đều ba cạnh AB, BC, CA. Chứng minh rằng I cách đều ba đỉnh A, B, C và cũng là trọng tâm của tam giác ABC. Đề bài Cho tam giác đều ABC có I là điểm cách đều ba cạnh AB, BC, CA. Chứng minh rằng I cách đều ba đỉnh A, B, C và cũng là trọng tâm của tam giác ABC. Phương pháp giải - Xem chi tiết Gọi M, N, P lần lượt là hình chiếu của I trên BC, AC, AB. Khi đó IM = IN = IP. +) Chứng minh I cách đều ba đỉnh của tam giác ABC. +) Chứng minh I là trọng tâm của tam giác ABC. Vậy I cách đều ba đỉnh A, B, C và cũng là trọng tâm của tam giác ABC Lời giải chi tiết Gọi M, N, P lần lượt là hình chiếu của I trên BC, AC, AB. Khi đó IM = IN = IP. +) Chứng minh I cách đều ba đỉnh của tam giác ABC. • Xét ∆AIP và ∆AIN có: \(\widehat {API} = \widehat {AQI}\) (cùng bằng 90°), AI là cạnh chung, IP = IN (chứng minh trên) Do đó ∆AIP = ∆AIN (cạnh huyền – cạnh góc vuông) Suy ra AP = AN (hai cạnh tương ứng) và \(\widehat {PAI} = \widehat {NAI}\) (hai góc tương ứng). Do đó AI là tia phân giác của góc BAC. Mà \(\widehat {BAC} = 60^\circ \) (do tam giác ABC đều). Nên \(\widehat {PAI} = \widehat {NAI} = 30^\circ \) Xét tam giác API vuông tại P có: \(\widehat {PAI} + \widehat {PIA} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°). Suy ra \(\widehat {PIA} = 90^\circ - \widehat {PAI} = 90^\circ - 30^\circ = 60^\circ \) Chứng minh tương tự ta có: \(\widehat {PIB} = 60^\circ \). Xét ∆PIA và ∆PIB có: \(\widehat {API} = \widehat {BPI} = 90^\circ \), PI là cạnh chung, \(\widehat {PIA} = \widehat {PIB}\) (cùng bằng 60°) Do đó ∆PIA = ∆PIB (cạnh góc vuông – góc nhọn kề). Suy ra IA = IB (hai cạnh tương ứng) • Chứng minh tương tự ta cũng có IB = IC. Do đó IA = IB = IC nên I cách đều ba đỉnh của tam giác ABC. +) Chứng minh I là trọng tâm của tam giác ABC. • Ta có ∆PIA = ∆PIB (chứng minh trên) Suy ra PA = PB (hai cạnh tương ứng). Do đó P là trung điểm của AB và điểm P cũng thuộc đường trung trực của AB. Lại có IA = IB nên điểm I thuộc đường trung trực của AB. CA = CB (do ∆ABC đều) nên điểm C thuộc đường trung trực của AB. Do đó ba điểm P, I, C thẳng hàng. Khi đó CP là đường trung truyến của tam giác ABC. • Chứng minh tương tự ta cũng có AM, BN là các đường trung tuyến của tam giác ABC. Mặt khác ba đường thẳng AM, BN, CP đều đi qua điểm I. Do đó I là trọng tâm tam giác ABC. Vậy I cách đều ba đỉnh A, B, C và cũng là trọng tâm của tam giác ABC.
|