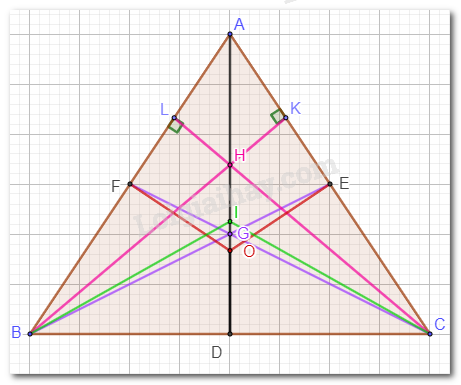
Giải bài 9 trang 120 SGK Toán 7 tập 2 - Cánh diềuCho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng: a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng; b) Nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A. Đề bài Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng: a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng; b) Nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A. Phương pháp giải - Xem chi tiết a) Trong tam giác cân: đường trung tuyến tại đỉnh cân đồng thời là đường cao và đường phân giác của góc tại đỉnh đó. b) Chứng minh tam giác ABC cân tại A, ta chứng minh AB = AC hoặc góc B bằng góc C. Lời giải chi tiết a)
Trong tam giác ABC cân tại A có AD là đường trung tuyến. Xét tam giác ABD và tam giác ACD có: AB = AC (tam giác ABC cân); AD chung; BD = DC (D là trung điểm của BC). Vậy \(\Delta ABD = \Delta ACD\)(c.c.c.). Suy ra: \(\widehat {ADB} = \widehat {ADC} = 90^\circ \) (vì ba điểm B, D, C thẳng hàng); \(\widehat {BAD} = \widehat {CAD}\). Vậy AD là đường cao của tam giác và đường phân giác của góc A. Suy ra: AD là đường trung trực của tam giác ABC. Vậy AD là đường trung tuyến, đường cao, đường phân giác, đường trung trực của tam giác ABC. Mà G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực nên A, G, H, I, O cùng nằm trên một đường thẳng. Vậy nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng. b)
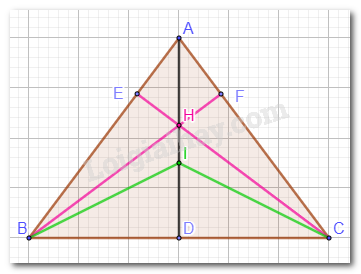
Ta có: \(AD \bot BC\). H là trực tâm của tam giác ABC nên A, H, D thẳng hàng. Mà A, H, I thẳng hàng nên A, H, I, K thẳng hàng. Suy ra: AD là tia phân giác của góc BAC (Vì AI là tia phân giác của góc BAC). Nên \(\widehat {BAD} = \widehat {CAD}\). Xét tam giác BAD và tam giác CAD có: \(\widehat {BAD} = \widehat {CAD}\); AD chung; \(\widehat {ADB} = \widehat {ADC}\) (\(AD \bot BC\)). \(\Rightarrow \Delta ABD = \Delta ACD\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng). Do đó, tam giác ABC cân tại A Vậy nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
|