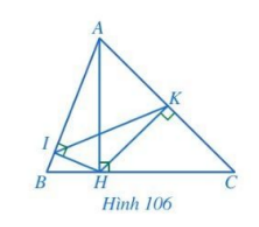
Giải bài 9 trang 95 SGK Toán 8 – Cánh diềuCho Hình 106. Chứng minh Đề bài Cho Hình 106. Chứng minh: a) \(A{H^2} = AB.AI = AC.AK\) b) \(\widehat {AIK} = \widehat {ACH}\)
Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Chứng minh \(\Delta AIH \backsim \Delta AHB\) và \(\Delta AKH \backsim \Delta AHC\) rồi suy ra các tỉ số đồng dạng. b) Chứng minh \(\Delta ABC \backsim \Delta AKI\) và suy ra các góc tương ứng. Lời giải chi tiết a) Xét tam giác AIH và tam giác AHB có: \(\widehat {AIH} = \widehat {AHB} = 90^\circ ,\,\,\widehat A\) chung \( \Rightarrow \Delta AIH \backsim \Delta AHB\) (g-g) \( \Rightarrow \frac{{AI}}{{AH}} = \frac{{AH}}{{AB}} \Rightarrow A{H^2} = AI.AB\) (1) Xét tam giác AKH và tam giác AHC có: \(\widehat {AKH} = \widehat {AHC} = 90^\circ ,\,\,\widehat A\) chung \( \Rightarrow \Delta AKH \backsim \Delta AHC\) (g-g) \( \Rightarrow \frac{{AK}}{{AH}} = \frac{{AH}}{{AC}} \Rightarrow A{H^2} = AK.AC\,\,\left( 2 \right)\) Từ (1) và (2) ta có: \(A{H^2} = AB.AI = AC.AK\) b) Theo câu a ta có \(AB.AI = AC.AK \Rightarrow \frac{{AB}}{{AK}} = \frac{{AC}}{{AI}}\) Xét tam giác ABC và tam giác AKI có: \(\frac{{AB}}{{AK}} = \frac{{AC}}{{AI}},\,\,\widehat A\) chung \( \Rightarrow \Delta ABC \backsim \Delta AKI\) (c-g-c) \( \Rightarrow \widehat {AIK} = \widehat {ACB} \Rightarrow \widehat {AIK} = \widehat {ACH}\)
|