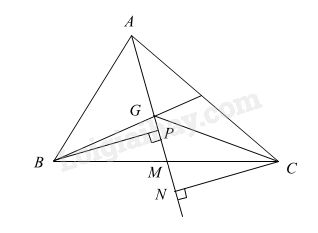
Giải bài 9.35 trang 83 SGK Toán 7 tập 2 - Kết nối tri thứcKí hiệu Đề bài Kí hiệu \({S_{ABC}}\) là diện tích tam giác ABC. Gọi G là trọng tâm tam giác ABC, M là trung điểm BC. a) Chúng minh \({S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\) Gợi ý: Sử dụng \(GM = \dfrac{1}{3}AM\) để chứng minh \({S_{GMB}} = \dfrac{1}{3}{S_{ABM}},{S_{GCM}} = \dfrac{1}{3}{S_{ACM}}\). b) Chứng minh \({S_{GCA}} = {S_{GAB}} = \dfrac{1}{3}{S_{ABC}}\). Phương pháp giải - Xem chi tiết a) Kẻ \(BP \bot AM\), \(CN \bot AM\) Sử dụng \(GM = \dfrac{1}{3}AM\) để chứng minh \({S_{GMB}} = \dfrac{1}{3}{S_{ABM}},{S_{GCM}} = \dfrac{1}{3}{S_{ACM}}\). b) -Chứng minh \({S_{GAB}} = {S_{GAC}}\) -Sử dụng \({S_{ABC}} = {S_{GAB}} + {S_{GAC}} + {S_{GBC}}\) Lời giải chi tiết
a) Vì G là trọng tâm tam giác ABC nên \(GM = \dfrac{1}{3}AM\) Kẻ \(BP \bot AM\) ta có \(\begin{array}{l}{S_{GMP}} = \dfrac{1}{2}BP.GM\\{S_{ABM}} = \dfrac{1}{2}BP.AM\end{array}\) Suy ra \(\dfrac{{{S_{GMP}}}}{{{S_{ABM}}}} = \frac{\dfrac{1}{2}BP.GM}{\dfrac{1}{2}BP.AM} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \) nên \({S_{GMP}} = \dfrac{1}{3}{S_{ABM}}\) (1) Tương tự, kẻ \(CN \bot AM\), ta có \(\begin{array}{l}{S_{GMC}} = \dfrac{1}{2}CN.GM\\{S_{ACM}} = \dfrac{1}{2}CN.AM\\ \text{nên} \,\dfrac{{{S_{GMC}}}}{{{S_{ACM}}}} = \frac{\dfrac{1}{2}CN.GM}{\dfrac{1}{2}CN.AM} = \dfrac{{GM}}{{AM}} = \dfrac{1}{3} \text{ suy ra }{S_{GMC}} = \dfrac{1}{3}{S_{ACM}}\left( 2 \right)\end{array}\) Cộng 2 vế của (1) và (2) ta có: \(\begin{array}{l}{S_{GMB}} + {S_{GMC}} = \dfrac{1}{3}\left( {{S_{AMC}} + {S_{ABM}}} \right)\\ \text{suy ra }{S_{GBC}} = \dfrac{1}{3}{S_{ABC}}\end{array}\) b) Xét \(\Delta BPM\) và \(\Delta CNM\) có: \(\widehat {BPM} = \widehat {CNM} = {90^0}\) BM = CM ( M là trung điểm của BC) \(\widehat {PMB} = \widehat {CMN}\) (2 góc đối đỉnh) nên \( \Delta BPM = \Delta CNM\) (cạnh huyền – góc nhọn) suy ra BP = CN (cạnh tương ứng) Mà \({S_{GAB}} = \dfrac{1}{2}BP.AG\), \({S_{GAC}} = \dfrac{1}{2}CN.AG\) Do đó \({S_{GAB}} = {S_{GAC}}\) Ta có: \(AG = \dfrac{2}{3}AM\) \(\begin{array}{l}{S_{ABC}} = {S_{GAB}} + {S_{GAC}} + {S_{GCB}}\\ {S_{ABC}} = {S_{GAB}} + {S_{GAC}} + \dfrac{1}{3}{S_{ABC}}\\ \text{nên } {S_{ABC}} - \dfrac{1}{3}{S_{ABC}} = 2{S_{GAC}} \\ \dfrac{2}{3}{S_{ABC}} = 2{S_{GAC}}\\ \text{suy ra }\dfrac{1}{3}{S_{ABC}} = {S_{GAC}} = {S_{GAB}}\end{array}\)
|