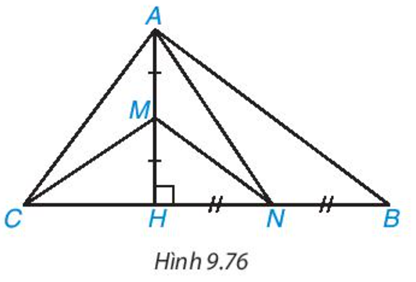
Giải bài 9.45 trang 111 SGK Toán 8 tập 2 - Kết nối tri thức

Đề bài

Cho tam giác ABC có đường cao AH. Biết AH=12cm, CH=9cm, BH=16cm. Lấy M, N lần lượt là trung điểm của AH, BH

a) Chứng minh rằng ABC là tam giác vuông tại A

b) Chứng minh rằng MN ⊥ AC và CM ⊥ AN

c) Tính diện tích tam giác AMN 

Lời giải chi tiết

a) Xét tam giác AHB vuông tại H, có:

$A{H^2} + H{B^2} = A{B^2}$ (định lý Pythagore)

=> $A{B^2} = {12^2} + {16^2}$

=> AB=20cm

Tương tự, có: $A{C^2} = A{H^2} + C{H^2}$ (áp dụng định lý Pythagore trong tam giác vuông AHC)

=> $A{C^2} = {12^2} + {9^2}$

=> AC=15cm

Có BC=9+16=25

Trong tam giác ABC, nhận thấy $A{B^2} + A{C^2} = B{C^2}$

=> Tam giác ABC vuông tại A

b) Xét tam giác AHB có: 

M là trung điểm của AH

B là trung điểm của BH

=> MN là đường trung bình của tam giác AHB

=> MN // AB

mà AB ⊥ AC (vì tam giác ABC vuông tại A)

=> MN ⊥ AC

Xét $\Delta ACN$ có $AH \bot CN$ (gt), $MN \bot AC$ (cmt), $AH \cap MN = M$. Vậy M là trực tâm của $\Delta ACN$, do đó $CM \bot AN$.

c) Ta có: ${S_{\Delta AMN}} = \frac{{AM.HN}}{2} = \frac{{\frac{{AH}}{2}.\frac{{BH}}{2}}}{2} = \frac{{AH.BH}}{8} = \frac{{12.16}}{8} = 24(c{m^2})$