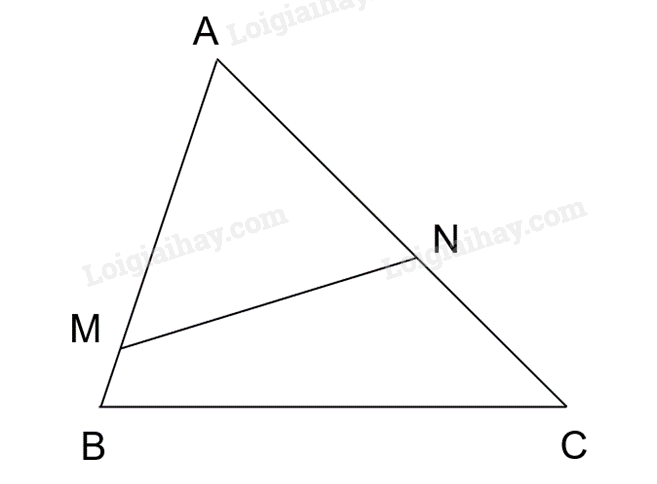
Giải bài 9.8 trang 90 SGK Toán 8 tập 2 - Kết nối tri thứcCho tam giác ABC có AB=12cm Đề bài Cho tam giác ABC có AB=12cm, AC=15cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM=10cm, AN=8cm. Chứng minh rằng ΔABC ∽ ΔANM. Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Chứng minh: \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\) - Chứng minh hai tam giác ABC và tam giác ANM có hai cạnh tương ứng tỉ lệ và góc A chung nên hai tam giác ABC và tam giác ANM đồng dạng với nhau. Lời giải chi tiết
Có AB=12cm , AN=8cm => \(\frac{{AN}}{{AB}} = \frac{8}{{12}} = \frac{2}{3}\) AC=15cm, AM=10cm => \(\frac{{AM}}{{AC}} = \frac{{10}}{{15}} = \frac{2}{3}\) => \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\) - Xét hai tam giác ABC và tam giác ANM, có \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\), góc A chung => ΔABC ∽ ΔANM (c.g.c)
|