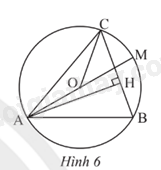
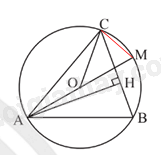
Giải bài tập 10 trang 82 SGK Toán 9 tập 2 - Chân trời sáng tạoCho tam giác nhọn ABC có đường cao AH (H ( in ) BC) và nội tiếp đường tròn tâm O có đường kính AM (hình 6). Chứng minh (widehat {OAC} = widehat {BAH}). Đề bài Cho tam giác nhọn ABC có đường cao AH (H \( \in \) BC) và nội tiếp đường tròn tâm O có đường kính AM (hình 6). Chứng minh \(\widehat {OAC} = \widehat {BAH}\).
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào góc nội tiếp chắn nửa đường tròn bằng 90o để chứng minh\(\widehat {OAC} + \widehat {OCM} = {90^o}\). Theo hình vẽ ta chứng minh \(\widehat {OAC} = \widehat {OCA} = {90^o} - \widehat {OCM} = \widehat {BAH}\) Lời giải chi tiết
OA = OC = R nên \(\Delta \)OAC cân tại O. Vì \(\widehat {ACM}\) là góc nội tiếp chắn cung AM, AM là đường kính đường tròn (O). Suy ra \(\widehat {ACM} = {90^o}\) hay \(\widehat {OAC} + \widehat {OCM} = {90^o}\) suy ra \(\widehat {OAC} = \widehat {OCA} = {90^o} - \widehat {OCM}\) Vì OC = OM = R nên tam giác OMC cân tại O suy ra \(\widehat {OCM} = \widehat {OMC}\). Do đó \(\widehat {OAC} = {90^o} - \widehat {OMC}\) Vì \(\widehat {OMC}\) và \(\widehat B\) cùng là góc nội tiếp chắn cung AC nhỏ nên \(\widehat {OAC} = {90^o} - \widehat {B} = \widehat {BAH}\) (tổng ba góc trong của tam giác).
|