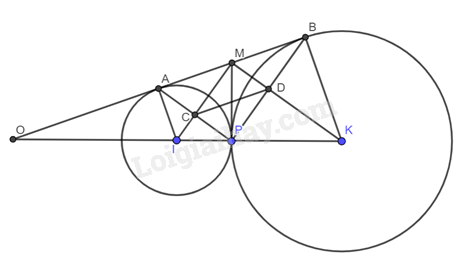
Giải bài tập 5 trang 124 SGK Toán 9 tập 1 - Cánh diềuCho hai đường tròn (left( {I;r} right)) và (left( {K;R} right)) tiếp xúc ngoài với nhau tại (P) với (R ne r), đường thẳng (a) lần lượt tiếp xúc với (left( {I;r} right)) và (left( {K;R} right)) tại (A) và (B,a) cắt (KI) tại (O). Đường thẳng qua (P) vuông góc với (IK) cắt đường thẳng (a) tại (M). Chứng minh: a) (frac{{OI}}{{OK}} = frac{r}{R}); b) (AB = 2MP); c) (widehat {IMK} = 90^circ ). Đề bài Cho hai đường tròn \(\left( {I;r} \right)\) và \(\left( {K;R} \right)\) tiếp xúc ngoài với nhau tại \(P\) với \(R \ne r\), đường thẳng \(a\) lần lượt tiếp xúc với \(\left( {I;r} \right)\) và \(\left( {K;R} \right)\) tại \(A\) và \(B,a\) cắt \(KI\) tại \(O\). Đường thẳng qua \(P\) vuông góc với \(IK\) cắt đường thẳng \(a\) tại \(M\). Chứng minh: a) \(\frac{{OI}}{{OK}} = \frac{r}{R}\); b) \(AB = 2MP\); c) \(\widehat {IMK} = 90^\circ \). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào kiến thức đã học để chứng minh. Lời giải chi tiết
a) Do \(AI\) là tiếp tuyến của \(\left( I \right)\) nên \(AI \bot AB\) Do \(BK\) là tiếp tuyến của \(\left( K \right)\) nên \(KB \bot AB\) Từ đó suy ra \(AI//BK\) Xét tam giác \(OBK\) có: \(AI//BK \) nên \(\frac{{OI}}{{OK}} = \frac{{AI}}{{BK}} = \frac{r}{R}\) (định lí Thalet). b) Xét \(\left( I \right)\) có \(MP,MA\) là hai tiếp tuyến cắt nhau nên \(MP = MA\)(1). Xét \(\left( K \right)\) có \(MP,MB\) là hai tiếp tuyến cắt nhau suy ra \(MP = MB\)(2). Từ (1) và (2) suy ra \(MP + MP = MA + MB \) hay \(2MP = AB\) c) Do \(AI//BK \) nên \(\widehat {OIA} = \widehat {IKB}\) (2 góc đồng vị). Mà \(\widehat {AIK} + \widehat {OAI} = 180^\circ \) (2 góc kề bù) nên \(\widehat {AIK} + \widehat {IKB} = 180^\circ \) (3). Do \(MP,MA\) là hai tiếp tuyến cắt nhau nên \(IM\) là phân giác \(\widehat {AIP} \), suy ra \(\widehat {MIP} = \frac{1}{2}\widehat {AIP}\) (4). Do \(MP,MB\) là hai tiếp tuyến cắt nhau nên \(KM\) là phân giác \(\widehat {IKP} \), suy ra \( \widehat {MKP} = \frac{1}{2}\widehat {IKP}\) (5). Từ (3), (4) và (5) suy ra \(\frac{1}{2}\widehat {AIP} + \frac{1}{2}\widehat {IKP} = \frac{1}{2}.180^\circ \) nên \(\widehat {MIP} + \widehat {MKP} = 90^\circ \) Xét tam giác \(IMK\) có: \(\widehat {MIP} + \widehat {MKP} = 90^\circ \) suy ra \(\widehat {IMK} = 90^\circ \)
|