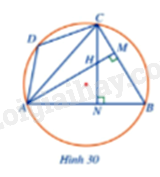
Giải bài tập 7 trang 78 SGK Toán 9 tập 2 - Cánh diềuCho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM, CN của tam giác ABC cắt nhau tại H (Hình 30). Chứng minh: a) (widehat {MHN} + widehat {ABC} = 180^circ .) b) (widehat {AHC} = widehat {ADC.}) c) (widehat {ADC} = widehat {BAM} + 90^circ .) Đề bài Cho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM, CN của tam giác ABC cắt nhau tại H (Hình 30). Chứng minh: a) \(\widehat {MHN} + \widehat {ABC} = 180^\circ .\) b) \(\widehat {AHC} = \widehat {ADC.}\) c) \(\widehat {ADC} = \widehat {BAM} + 90^\circ .\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Áp dụng tổng 4 góc trong tứ giác HMBN bằng \(180^\circ \) b) \(\widehat {AHC} = \widehat {ADC}\) vì cùng bù với góc CBA. c) Chứng minh \(\widehat {BAM} + \widehat {AMB} = \widehat {BAM} + 90^\circ = 180^\circ - \widehat {MBA} = \widehat {ADC}.\) Lời giải chi tiết
a) Do tam giác ABC có hai đường cao AM, CN nên \(\widehat {HMB} = 90^\circ ,\widehat {BNH} = 90^\circ \) Xét tứ giác HMBN có: \(\begin{array}{l}\widehat {NHM} + \widehat {HMB} + \widehat {MBN} + \widehat {BNH} = 360^\circ \\\widehat {NHM} + \widehat {MBN} = 360^\circ - \widehat {HMB} - \widehat {BNH}\\\widehat {NHM} + \widehat {MBN} = 360^\circ - 90^\circ - 90^\circ = 180^\circ .\end{array}\) Hay \(\widehat {MHN} + \widehat {ABC} = 180^\circ .\) b) Vì ABCD nội tiếp đường tròn nên \(\widehat {CDA} + \widehat {ABC} = 180^\circ .\) mà \(\widehat {MHN} + \widehat {ABC} = 180^\circ \) (câu a) suy ra \(\widehat {CDA} = \widehat {MHN}\), hơn nữa \(\widehat {CHA} = \widehat {MHN}\) (đối đỉnh) vậy \(\widehat {CHA} = \widehat {CDA.}\) c) Xét tam giác AMB vuông tại M có: \(\widehat {BAM} + \widehat {AMB} = \widehat {BAM} + 90^\circ = 180^\circ - \widehat {MBA.}\) Mà \(180^\circ - \widehat {MBA} = \widehat {ADC}\) (do ABCD nội tiếp) Vậy \(\widehat {ADC} = \widehat {BAM} + 90^\circ .\)
|