Giải bài tập 7.29 trang 55 SGK Toán 9 tập 2 - Kết nối tri thứcQua đợt khám mắt, lớp 9A có 20 học sinh bị cận thị trong đó có 10 học sinh bị cận thị nhẹ, 8 học sinh cận thị vừa và 2 học sinh cận thị nặng. Biết rằng cận thị có số đo từ 0,25 đến dưới 3,25 dioptre là cận thị nhẹ, từ 3,25 đến dưới 6,25 dioptre là cận thị vừa; từ 6,25 đến dưới 10,25 dioptre là cận thị nặng. a) Lập bảng tần số và bảng tần số tương đối ghép nhóm theo độ cận thị của các học sinh này. b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho bảng tần số tương đối ghép nhóm thu Đề bài Qua đợt khám mắt, lớp 9A có 20 học sinh bị cận thị trong đó có 10 học sinh bị cận thị nhẹ, 8 học sinh cận thị vừa và 2 học sinh cận thị nặng. Biết rằng cận thị có số đo từ 0,25 đến dưới 3,25 dioptre là cận thị nhẹ, từ 3,25 đến dưới 6,25 dioptre là cận thị vừa; từ 6,25 đến dưới 10,25 dioptre là cận thị nặng. a) Lập bảng tần số và bảng tần số tương đối ghép nhóm theo độ cận thị của các học sinh này. b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho bảng tần số tương đối ghép nhóm thu được ở câu a. Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Bảng tần số ghép nhóm: + Tìm tần số của từng nhóm: Tần số \({m_i}\) của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) là số giá trị của mẫu số liệu lớn hơn hoặc bằng \({a_i}\) và nhỏ hơn \({a_{i + 1}}\). + Lập bảng tần số ghép nhóm:
Bảng tần số tương đối ghép nhóm: + Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu. + Lập bảng tần số tương đối ghép nhóm:
b) Cách vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng: Bước 1: Chọn giá trị \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) đại diện cho các nhóm số liệu \(\left[ {{a_i};{a_{i + 1}}} \right)\) với \(i = 1,2,3,..,k\). Bước 2: Vẽ trục ngang để biểu diễn các giá trị đại diện cho nhóm số liệu, vẽ trục đứng thể hiện tần số tương đối. Bước 3: Với mỗi giá trị đại diện \({x_i}\) trên trục ngang và tần số tương đối \({f_i}\) tương ứng, ta xác định một điểm \({M_i}\left( {{x_i};{f_i}} \right)\). Nối các điểm liên tiếp với nhau. Bước 4: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ. Lời giải chi tiết a) Vì có 10 học sinh có số đo từ 0,25 đến dưới 3,25 dioptre; 8 học sinh có số đo từ 3,25 đến dưới 6,25 dioptre và 2 học sinh có số đo từ 6,25 đến dưới 10,25 dioptre nên ta có bảng tần số ghép nhóm:
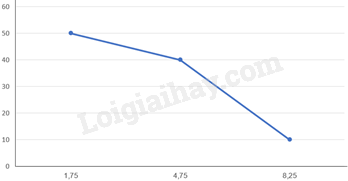
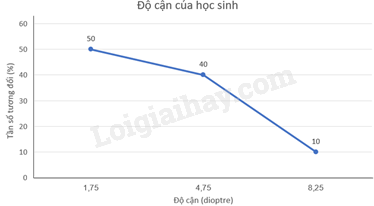
Tần số tương đối của các nhóm \(\left[ {0,25;3,25} \right)\); \(\left[ {3,25;6,25} \right)\); \(\left[ {6,25;10,25} \right)\) lần lượt là: \(\frac{{10}}{{20}} = 50\% ;\frac{8}{{20}} = 40\% ;\frac{2}{{20}} = 10\% \) Ta có bảng tần số tương đối ghép nhóm theo độ cận thị của các học sinh này là:
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng: Bước 1: Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:
Bước 2: Vẽ các trục. Bước 3: Xác định các điểm, nối các điểm liên tiếp với nhau.
Bước 4: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ tần số tương đối ghép nhóm.
|