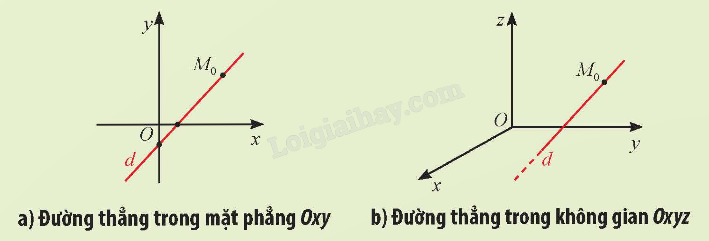
Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạoTa đã biết trong mặt phẳng Oxy, phương trình tham số của đường thẳng có dạng: Đề bài Ta đã biết trong mặt phẳng Oxy, phương trình tham số của đường thẳng có dạng: \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\end{array} \right.\) \(\left( {{a_1}^2 + {a_2}^2 \ne 0,t \in \mathbb{R}} \right)\). Trong không gian Oxyz, phương trình tham số của đường thẳng có dạng như thế nào?
Phương pháp giải - Xem chi tiết Sử dụng kiến thức đã học. Lời giải chi tiết Trong không gian Oxyz, phương trình tham số của đường thẳng d đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\overrightarrow a = \left( {{a_1};{a_2};{a_3}} \right)\) làm vecto chỉ phương có dạng \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\) với \(t \in \mathbb{R}\) (t được gọi là tham số).
|