Giải câu hỏi trắc nghiệm trang 13, 14 vở thực hành Toán 7Giá trị của \({\left( {{2^3}} \right)^5}\) :
Lựa chọn câu để xem lời giải nhanh hơn
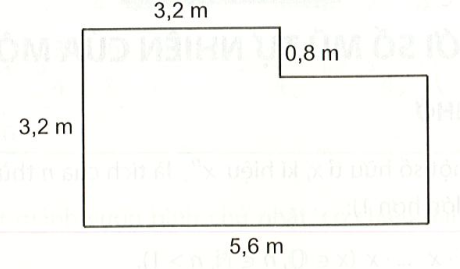
Câu 1 trang 13 Giá trị của \({\left( {{2^3}} \right)^5}\) : A.\({2^8};\) B.\({2^{15}};\) C.\({\left( {\frac{1}{2}} \right)^{28}};\) D.\(\frac{1}{2}\) Phương pháp giải: -Sử dụng công thức tính lũy thừa của lũy thừa. Lời giải chi tiết: Đáp án đúng là B Ta có: \({\left( {{2^3}} \right)^5} = {2^{3.5}} = {2^{15}}.\) Câu 2 trang 13 Giá trị của \({\left( {\frac{1}{2}} \right)^7}:{\left( {\frac{1}{2}} \right)^4}\) là: A.\({\left( {\frac{1}{2}} \right)^{11}};\) B.\(\frac{1}{8};\) C.\({\left( {\frac{1}{2}} \right)^{28}};\) D.\(\frac{1}{2}.\) Phương pháp giải: - Ta sẽ sử dụng \({a^m} - {a^n} = {a^{m - n}}.\) - Rồi sau đó ta sẽ tính lũy thừa Lời giải chi tiết: Đáp án đúng là B \({\left( {\frac{1}{2}} \right)^7}:{\left( {\frac{1}{2}} \right)^4} = {\left( {\frac{1}{2}} \right)^{7 - 4}} = {\left( {\frac{1}{2}} \right)^3} = \frac{1}{8}.\) Câu 3 trang 14 Diện tích của hình sau bằng A.\(16{m^2};\) B.\(17,92{m^2};\) C.\(35,84{m^2};\) D.\(24{m^2}.\) Phương pháp giải: -Ta sẽ chia hình thành 2 hình chữ nhật nhỏ rồi sau đó tính diện tích từng hình -Rồi diện tích hình lớn bằng tổng diện tích 2 hình nhỏ. Lời giải chi tiết: Đáp án đúng là A. Xét hình chữ nhật \(ABCD\) có chiều dài\(AB = 3,2m\) và chiều rộng \(BC = 0,8m.\) Diện tích hình chữ nhật \(ABCD\) là: \(3,2.0,8 = 2,56{m^2}.\) Xét hình chữ nhật \(DGFE\) có chiều dài \(EF = 5,6m\) và chiều rộng \(DE = AE - AD = 3,2 - 0,8 = 2,4m.\) Diện tích hình chữ nhật \(DGFE\) là: \(2,4.5,6 = 13,44{m^2}.\) Diện tích của hình bằng tổng diện tích của hình chữ nhật \(ABCD\) và \(DGFE\) và bằng: \(2,56 + 13,44 = 16{m^2}.\) Câu 4 trang 14 Giá trị của \(n\) bằng bao nhiêu nếu\({\left( {\frac{1}{3}} \right)^{n + 1}} = \frac{1}{{81}}.\) A.2. B.4. C.1. D.3. Phương pháp giải: -Ta sẽ quy đổi \(\frac{1}{{81}}\) bằng \(\frac{1}{3}\) mũ mấy đó -Ta sẽ cho \(n + 1\) bằng số mũ vừa tìm, từ đó suy ra \(n\) Lời giải chi tiết: Đáp án đúng là D. Ta có:\(\begin{array}{l}{\left( {\frac{1}{3}} \right)^{n + 1}} = \frac{1}{{81}}\\ \Leftrightarrow {\left( {\frac{1}{3}} \right)^{n + 1}} = {\left( {\frac{1}{3}} \right)^4}\\ \Leftrightarrow n + 1 = 4\\ \Leftrightarrow n = 3\end{array}\) Vậy\(n = 3.\)
|