Giải câu hỏi trang 66, 67, 68 SGK Toán 8 – Cánh diềuTrong Hình 38, tam giác ABC có AD là đường phân giác của góc BAC.
Lựa chọn câu để xem lời giải nhanh hơn
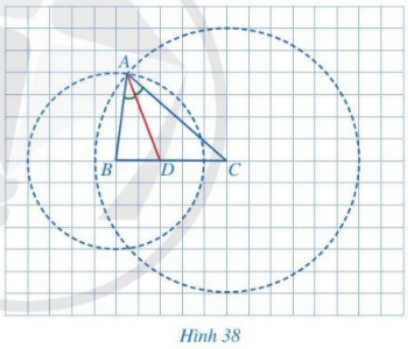
HĐ1 Video hướng dẫn giải Trong Hình 38, tam giác ABC có AD là đường phân giác của góc BAC. Giả sử mỗi ô vuông của lưới ô vuông có độ dài cạnh bằng 1 cm. a) Tính độ dài các đoạn thẳng DB, DC. b) Tính độ dài các đoạn thẳng AB, AC. c) So sánh các tỉ số \(\frac{{DB}}{{DC}},\,\,\frac{{AB}}{{AC}}\).
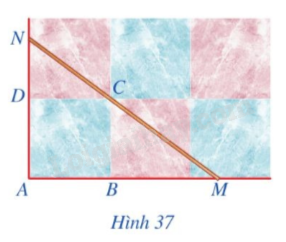
Phương pháp giải: a) Đếm số ô tương ứng với các đoạn thẳng và tính độ dài. b) AB và AC là bán kính của hai đường tròn. c) Tính hai tỉ số và so sánh chúng. Lời giải chi tiết: a) Ta thấy mỗi ô vuông có độ dài cạnh bằng 1cm. Đoạn thẳng BD có độ dài bằng độ dài cạnh của 2 ô vuông nên BD dài 2 cm. Đoạn thẳng DC có độ dài bằng độ dài cạnh của 3 ô vuông nên BD dài 3 cm. b) Ta thấy AB là bán kính đường tròn tâm B. Mà bán kính đường tròn tâm B có độ dài 4 ô vuông, tương ứng với 4 cm nên AB dài 4 cm. Ta thấy AC là bán kính đường tròn tâm C. Mà bán kính đường tròn tâm C có độ dài 6 ô vuông, tương ứng với 6 cm nên AB dài 6 cm. c) Ta có: \(\frac{{DB}}{{DC}} = \frac{2}{3};\,\,\frac{{AB}}{{AC}} = \frac{4}{6} = \frac{2}{3}\) Vậy \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\). LT1 Video hướng dẫn giải Giải bài toán nêu trong phần mở đầu. Bài toán: Hình 37 minh họa một phần sân nhà bạn Duy được lát bởi các viên gạch hình vuông khít nhau, trong đó các điểm A, B, C, D là bốn đỉnh của một viên gạch. Bạn Duy đặt một thước gỗ trên mặt sân sao cho thước gỗ luôn đi qua điểm C và cắt tia AB tại M, cắt tia AD tại N. Bạn Duy nhận thấy ta luôn có tỉ lệ thức \(\frac{CM}{CN} = \frac{AM}{AN}\)
Phương pháp giải: Dựa vào tính chất đường phân giác để chứng minh. Lời giải chi tiết: Ta có ABCD là hình vuông có AC là đường chéo nên góc DAC bằng góc CAB. Hay góc NAC bằng góc MAC. Suy ra: AC là đường phân giác của góc MAN. Theo định lí đường phân giác của tam giác ta có: \(\frac{CM}{CN} = \frac{AM}{AN}\) LT2 Video hướng dẫn giải Cho tam giác ABC có \(AB < AC\), AD là đường phân giác. Chứng minh \(DB < DC\). Phương pháp giải: Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài. Lời giải chi tiết:
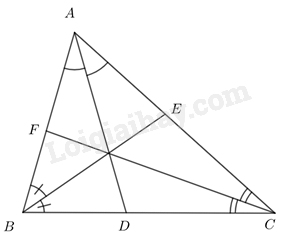
Xét tam giác ABC có AD là đường phân giác nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\) Mà \(AB < AC\)\( \Rightarrow \frac{{AB}}{{AC}} < 1 \Rightarrow \frac{{DB}}{{DC}} < 1 \Rightarrow DB < DC\). LT3 Video hướng dẫn giải Cho tam giác ABC có ba đường phân giác AD, BE, CF. Chứng minh \(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = 1\) Phương pháp giải: Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài. Lời giải chi tiết:
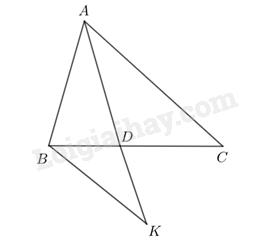
Xét tam giác ABC với ba đường phân giác AD, BE, CF, ta có: \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}};\,\,\frac{{BC}}{{BA}} = \frac{{EC}}{{EA}};\,\,\frac{{CA}}{{CB}} = \frac{{FA}}{{FB}}\) (Tính chất đường phân giác) \( \Rightarrow \frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{{AB}}{{AC}}.\frac{{BC}}{{BA}}.\frac{{CA}}{{CB}} = \frac{{AB.BC.CA}}{{CA.AB.BC}} = 1\) (đpcm). LT4 Video hướng dẫn giải Cho tam giác ABC, điểm D thuộc cạnh BC sao cho \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\). Chứng minh AD là tia phân giác của góc BAC. Phương pháp giải: Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài. Lời giải chi tiết:
Từ B kẻ đường thẳng song song với AC, cắt AD tại K. Vì \(BK//AC\) nên theo hệ quả của định lý Thales, ta có: \(\frac{{DB}}{{DC}} = \frac{{BK}}{{AC}}\) Mà \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) nên \(\frac{{BK}}{{AC}} = \frac{{AB}}{{AC}} \Rightarrow AB = BK\) Khi đó tam giác ABK cân tại B nên \(\widehat {BAK} = \widehat {BKA}\) Mà \(BK//AC\) nên \(\widehat {BKA} = \widehat {KAC}\) \( \Rightarrow \widehat {BAK} = \widehat {KAC}\) Vậy AD là đường phân giác trong tam giác ABC.
|