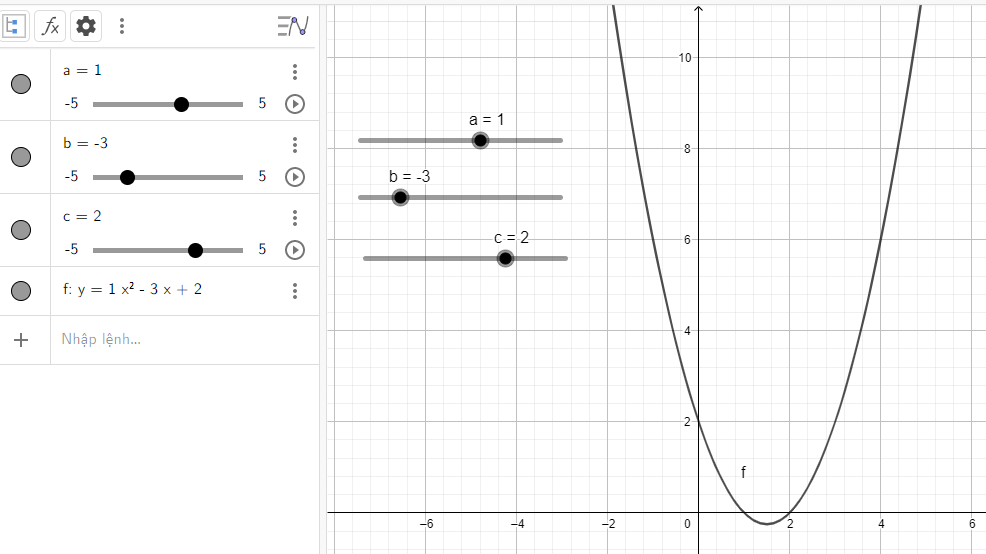
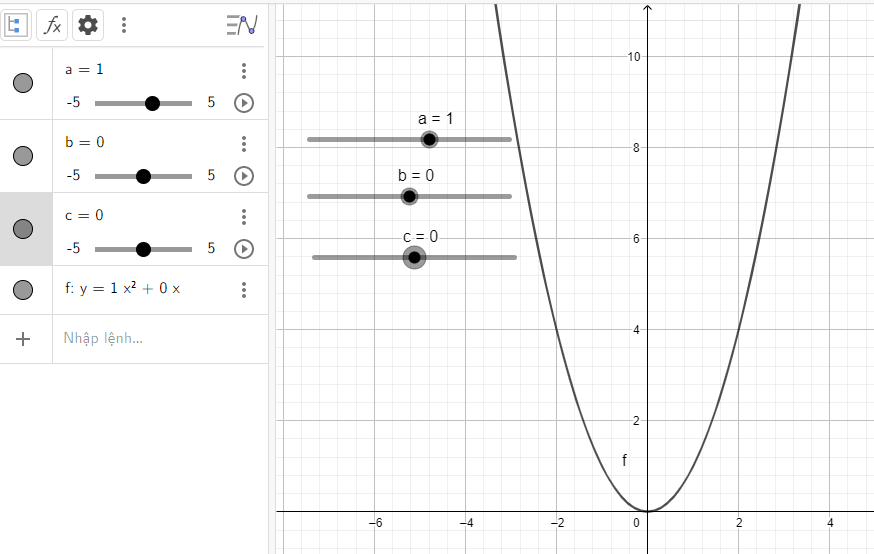
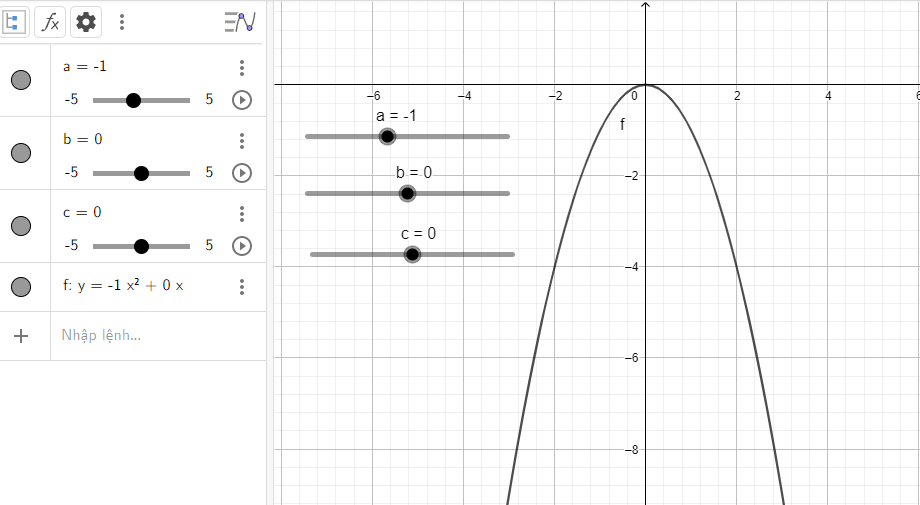
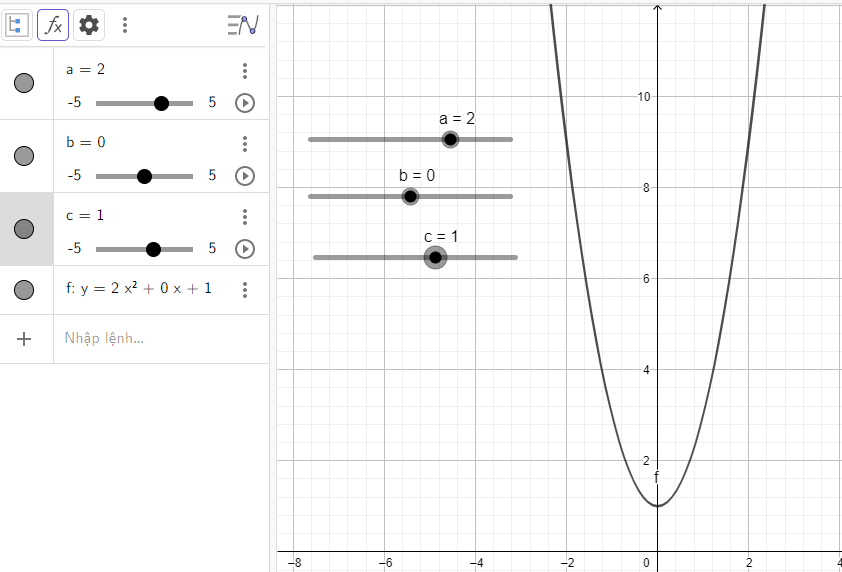
Giải Hoạt động 2 trang 89 SGK Toán 10 tập 2 - Chân trời sáng tạoĐiều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau: Đề bài Thực hành 2 trang 89 SGK Toán 10 tập 2 – CTST Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau: a) \(\)\(y = {x^2} - 3x + 2\) b) \(y = {x^2}\) c) \(y = - {x^2}\) d) \(y = 2{x^2} + 1\) e) \(y = - \frac{1}{2}{x^2} + 4\) Phương pháp giải - Xem chi tiết Bước 1: Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online Bước 2: Tạo các thanh trượt biểu thị các tham số a, b, c bằng cách nhấp chuật liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt (hình 4) +) Nhập công thúc hàm số bậc hai \(y = a{x^2} + bx + c\) tại vùng nhập lệnh theo cú pháp: y = ax^2 + bx + c +) Nhập công thức \(\Delta = {b^2} - 4ac\) bằng cách gõ: D = b^2 - 4ac +) Quan sát đồ thị được vẽ trên vùng làm việc +) Dùng chuột điều chỉnh các thanh trượt a, b, c để có giá trị mong muốn +) Quan sát sự thay đổi của hình dạng đồ thị (parabol) và \(\Delta \) theo sự thay đổi các hệ số a, b, c trong công thức hàm số Bước 3: Nêu kết luận về tính chất của đồ thị quan sát được trên hình vẽ Lời giải chi tiết Thực hiện các bước đã nêu ở phương pháp ta có các hình dưới đây a) Quan sát vào đồ thị ta thấy: Đồ thị quay bề lõm về phía trên, cắt trục tung và trục hoành lần lượt tại điểm có tọa độ là (0; 2) và (2; 0) b) Quan sát vào đồ thị ta thấy: Đồ thị quay bề lõm về phía trên, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ c) Quan sát vào đồ thị ta thấy: Đồ thị quay bề lõm về phía dưới, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ d) Quan sát vào đồ thị ta thấy: Đồ thị quay bề lõm về phía trên, cắt trục tung tại điểm có tung độ là 1 đó cũng chính là đỉnh của parabol
e) Quan sát vào đồ thị ta thấy: Đồ thị quay bề lõm về phía dưới, cắt trục tung tại điểm có tung độ là 4 đó cũng chính là đỉnh của parabol
|