Giải mục 1 trang 38, 39, 40 SGK Toán 10 tập 2 - Chân trời sáng tạoTrong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ OM Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc 30 (hình 7) a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD
Lựa chọn câu để xem lời giải nhanh hơn
HĐ Khởi động
Lời giải chi tiết: Bàn cờ được chia thành 8 hàng (1-8) và 8 cột (a-h) đánh số như hình vẽ. Do đó mỗi quân cờ xác định khi biết số hàng và số cột, tương ứng với cặp số (x;y) trong đó x là số hàng, y là số cột. Khi đó hai mã đen có vị trí là (8;b) và (4;e) Hai mã trắng có vị trí là (3;c) và (3;f) Cách 2: Đặt gốc tọa độ tại góc dưới, bên trái của bàn cờ. Coi mỗi ô vuông là 1 đơn vị. Ta xác định được tọa độ của các con mã như sau: Hai mã đen có tọa độ lần lượt là (2;8), (5;4) Hai mã trắng có tọa độ lần lượt là (3;3) và (6;3) HĐ Khám phá 1 Nêu nhận xét về độ lớn, phương và chiều của vectơ trên trục \(Ox\) và vectơ \(\overrightarrow j \) trên trục \(Oy\) (hình 1)
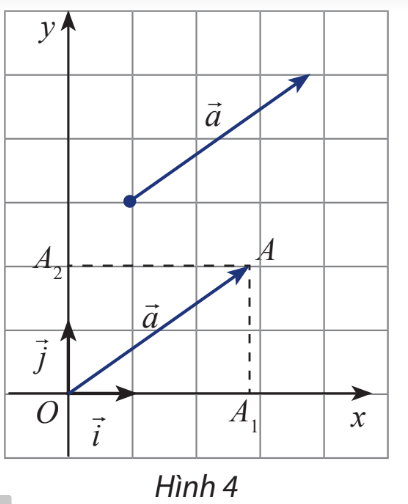
Lời giải chi tiết: +) Vectơ có độ lớn bằng 1 đơn vị, phương song song với trục \(Ox\)và cùng chiều với \(Ox\) +) Vectơ \(\overrightarrow j \) có độ lớn bằng 1 đơn vị, phương song song với trục \(Oy\)và cùng chiều với \(Oy\) HĐ Khám phá 2 Trong mặt phẳng Oxy, cho một vectơ \(\overrightarrow a \)tùy ý. Vẽ \(\overrightarrow {OA} = \overrightarrow a \)và gọi \({A_1},{A_2}\)lần lượt là hình chiếu vuông góc của A lên Ox và Oy (hình 4). Đặt \({\overrightarrow {OA} _1} = x\overrightarrow i \), \({\overrightarrow {OA} _2} = y\overrightarrow j \). Biểu diễn vectơ \(\overrightarrow a \)theo hai vectơ và \(\overrightarrow j \)
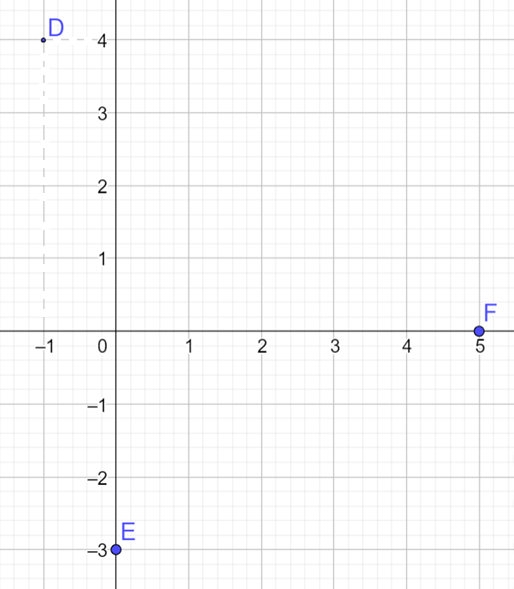
Phương pháp giải: Bước 1: Áp dụng quy tắc hình bình hành \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \) Bước 2: Dựa vào hình vẽ tìm x,y Bước 3: Biểu diễn vectơ \(\overrightarrow a \) Lời giải chi tiết: Áp dụng quy tắc hình bình hành ta có \(\overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} \) Dựa vào hình vẽ ta thấy \({\overrightarrow {OA} _1} = 3\overrightarrow i \) và \({\overrightarrow {OA} _2} = 2\overrightarrow j \) Vậy \(\overrightarrow a = \overrightarrow {OA} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} = 3\overrightarrow i + 2\overrightarrow j \) HĐ Khám phá 3 Trong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ \(\overrightarrow {OM} \) Phương pháp giải: Bước 1: Từ điểm M(x;y) xác định \({M_1},{M_2}\) lần lượt là hình chiếu vuông góc của M xuống trục hoành và trục tung Bước 2: Tìm m, n sao cho \( \overrightarrow {OM_1}= m.\overrightarrow {i}; \, \overrightarrow {OM_2}=n.\overrightarrow {j} \) Bước 3: Dựa vào quy tắc hình bình hành, suy ra tọa độ của vectơ \(\overrightarrow {OM}\) theo \( \overrightarrow {i}; \overrightarrow {j}\). Lời giải chi tiết: Cho điểm M(x;y) bất kì, xác định \({M_1},{M_2}\) lần lượt là hình chiếu vuông góc của M xuống trục hoành và trục tung Dễ thấy \(\overrightarrow {O{M_1}}= x\overrightarrow i ; \, \overrightarrow {O{M_2}} = y \overrightarrow j \) Áp dụng quy tắc hình bình hành ta có \(\overrightarrow {OM} = \overrightarrow {O{M_1}} + \overrightarrow {O{M_2}} = x\overrightarrow i + y\overrightarrow j \) Vậy tọa độ của vectơ \(\overrightarrow {OM} \) là (x;y), trùng với tọa độ điểm M. Thực hành 1 Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\) a) Vẽ các điểm D, E, F trên mặt phẳng Oxy b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \). c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy Lời giải chi tiết: a)
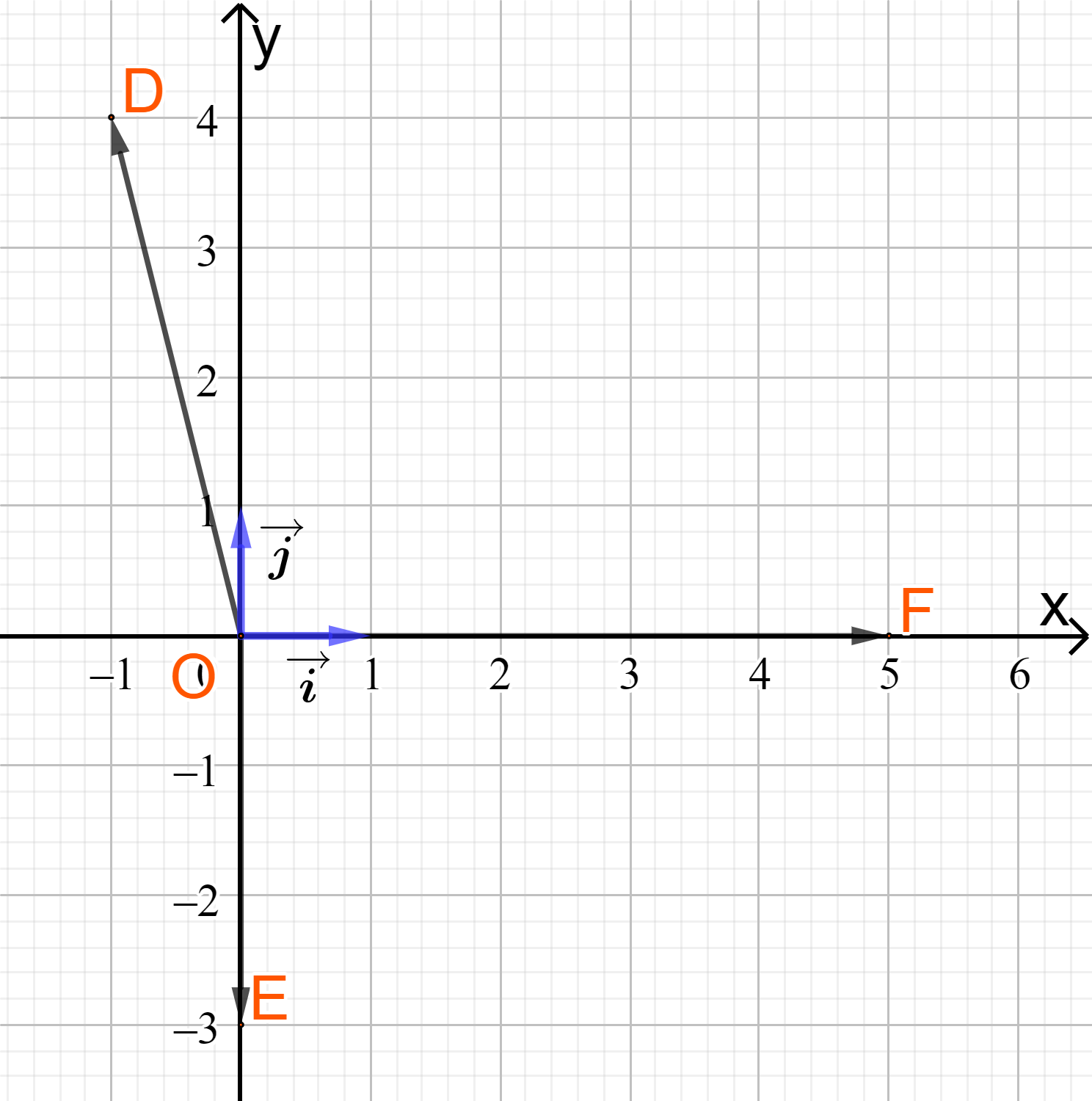
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có: \(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\) c)
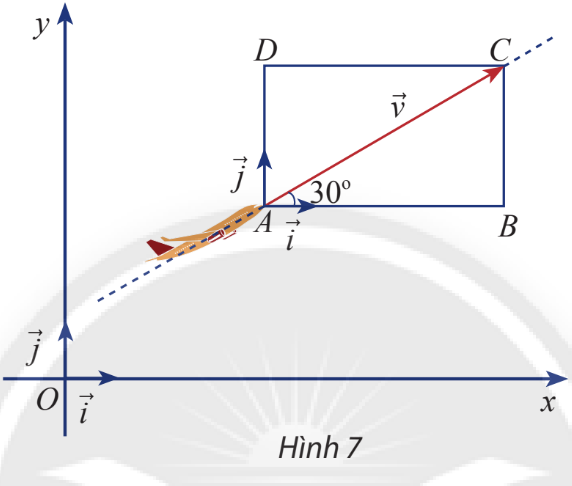
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là và \(\overrightarrow j = (0;1)\) Vận dụng 1 Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc \(30^\circ \) (hình 7) a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD b) Biểu diễn vận tốc \(\overrightarrow v \) theo hai vectơ và \(\overrightarrow j \) c) Tìm tọa độ của \(\overrightarrow v \)
Lời giải chi tiết: a) Vận tốc 240 km/h nên \(\left| {\overrightarrow v } \right| = AC = 240\) Áp dụng các tính chất trong tam giác vuông ta có \(AB = DC = AC.\cos (\widehat {CAB}) = 240.\cos (30^\circ ) = 120{\sqrt 3 }\) \(AD = BC = AC.\sin (\widehat {CAB}) = 240.\sin (30^\circ ) = 120\) b) Xem A là gốc tọa độ nên ta có \(\overrightarrow {AB} = 120\overrightarrow i ,\overrightarrow {AD} = 120{\sqrt 3 }\overrightarrow j ,\overrightarrow v = \overrightarrow {AC} = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \) c) Ta có \(\overrightarrow v = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \) Vậy tọa độ của vectơ \(\overrightarrow v \) là \(\left( {120;120{\sqrt 3 }} \right)\)
|