Giải mục 1 trang 98, 99, 100 SGK Toán 8 tập 2 - Kết nối tri thứcHãy chỉ ra hai cặp tam giác vuông đồng dạng có trong hình 9.48:
Lựa chọn câu để xem lời giải nhanh hơn
CH1 Video hướng dẫn giải Hãy chỉ ra hai cặp tam giác vuông đồng dạng có trong hình 9.48:
Phương pháp giải: Sử dụng các trường hợp đồng dạng của tam giác. Lời giải chi tiết: Các cặp tam giác vuông đồng dạng: \(\begin{array}{l}\Delta ABC \backsim \Delta X{{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{{D}}F \backsim \Delta KGH\left( {\frac{{E{{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{{D}}F} = \widehat {KGH}} \right)\end{array}\) LT1 Video hướng dẫn giải Nam và Việt muốn đo chiều cao của cột cờ ở sân trường mà hai bạn không trèo lên được. Vào buổi chiều, Nam đo thấy bóng của cột cờ dài 6m và bóng của Việt dài 70cm. Nam hỏi Việt cao bao nhiêu, Việt trả lời là cao 1,4m. Nam liền reo lên: "Tớ biết cột cờ cao bao nhiêu rồi đấy" Vậy cột cờ cao bao nhiêu và làm sao bạn Nam biết được. Ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc vuông của tam giác ABC vuông tại đỉnh A, bạn Việt và bóng của mình cũng được xem là hai canh góc vuông của tam giác A'B'C' vuông tại đỉnh A'. Vì các tia sáng mặt trời tạo với hai cái bóng các góc bằng nhau nên \(\widehat B = \widehat {B'}\) a) Hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không? b) Bạn Nam đã tính chiều cao chiếc cột, tức là độ dài đoạn thẳng AC như thế nào và kết quả là bao nhiêu?
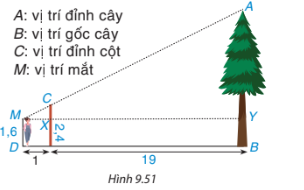
Phương pháp giải: Chứng minh ΔABC ∽ ΔA′B′C′ suy ra các tỉ số đồng dạng và tính AC Lời giải chi tiết: a) Hai tam giác vuông ABC và A'B'C' có \(\widehat B = \widehat {B'}\) => ΔABC ∽ ΔA′B′C′ b) Vì ΔABC ∽ ΔA′B′C′ nên \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) hay \(\frac{{0,7}}{6} = \frac{{1,4}}{{AC}}\) suy ra AC=12(m) TTN Video hướng dẫn giải Một người đo chiều cao của một cái cây bằng cách cắm một chiếc cọc xuống đất, cọc cao 2,4m và cách vị trí gốc cây 19m. Người đo đứng cách xa chiếc cọc 1m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chấn đến mắt người ấy là 1,6m(H9.51) A: Vị trí đỉnh cây B: Vị trí gốc cây C: Vị trí đỉnh cột. D: Vị trí mắt
Phương pháp giải: Chứng minh tam giác MXC đồng dạng với tam giác MYA rồi suy ra các tỉ số đồng dạng. Tính được chiều cao của cây. Lời giải chi tiết: Ta có: CX = 2,4 – 1,6 = 0,8(m) MY = 1 + 19 = 20 (m) Xét tam giác MXC và tam giác MYA có: góc M chung; \(\widehat {M{{X}}C} = \widehat {MY{{A}}}\) nên \( \Delta M{{X}}C \backsim \Delta MY{{A}}\) suy ra \(\frac{{M{{X}}}}{{MY}} = \frac{{XC}}{{Y{{A}}}}\) hay \(\frac{1}{{20}} = \frac{{0,8}}{{Y{{A}}}}\) nên \(Y{{A}} = 20.0,8 = 16(m)\) Vậy chiều cao của cây là: \(AB = BY + Y{{A}} = 1,6 + 16 = 17,6(m)\)
|