Giải mục 2 trang 33, 34 SGK Toán 12 tập 2 - Chân trời sáng tạo

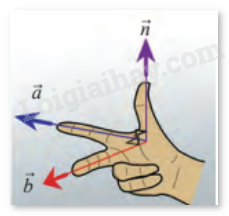
HĐ1

Trả lời câu hỏi Hoạt động 2 trang 33, 34 SGK Toán 12 Chân trời sáng tạo

Trong không gian $Oxyz$, cho mặt phẳng $\left( \alpha  \right)$ có cặp vectơ chỉ phương $\vec a = \left( {{a_1};{a_2};{a_3}} \right)$, $\vec b = \left( {{b_1};{b_2};{b_3}} \right)$. Xét vectơ $\vec n = \left( {{a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1}} \right)$.

a) Vectơ $\vec n$ có khác $\vec 0$ hay không?

b) Tính $\vec a.\vec n$; $\vec b.\vec n$.

c) Vectơ $\vec n$ có phải là vectơ pháp tuyến của mặt phẳng $\left( \alpha  \right)$ không?

Phương pháp giải:

a) Giả sử $\vec n = \vec 0$, sau đó chứng minh rằng $\vec a$ và $\vec b$ là hai vectơ cùng phương. Điều này là vô lí do $\vec a$ và $\vec b$ là một cặp vectơ chỉ phương của $\left( \alpha  \right)$.

b) Sử dụng công thức tích vô hướng của hai vectơ trong không gian.

c) Để chứng minh $\vec n$ là vectơ pháp tuyến của mặt phẳng $\left( \alpha  \right)$, ta chỉ ra rằng $\vec n$ có giá vuông góc với mặt phẳng $\left( \alpha  \right)$.

Lời giải chi tiết:

a) Giả sử $\vec n = \vec 0$, khi đó ${a_2}{b_3} - {a_3}{b_2} = {a_3}{b_1} - {a_1}{b_3} = {a_1}{b_2} - {a_2}{b_1} = 0$.

Với trường hợp ${b_1}$, ${b_2}$, ${b_3}$ cùng khác 0, ta suy ra $\frac{{{a_1}}}{{{b_1}}} = \frac{{{a_2}}}{{{b_2}}} = \frac{{{a_3}}}{{{b_3}}}$, điều này có nghĩa $\vec a$ và $\vec b$ là hai vectơ cùng phương.

Nếu ${b_1} = 0$ thì ${a_1} = 0$, ta vẫn thu được kết quả $\vec a$ và $\vec b$ là hai vectơ cùng phương.

Các trường hợp còn lại cho ra kết quả tương tự.

Như vậy $\vec a$ và $\vec b$ là hai vectơ cùng phương.

Mặt khác, do $\vec a$ và $\vec b$ là một cặp vectơ chỉ phương của $\left( \alpha  \right)$, nên $\vec a$ và $\vec b$ là hai vectơ không cùng phương, mâu thuẫn.

Như vậy $\vec n \ne \vec 0$.

b) Ta có:

+)$\vec a.\vec n = {a_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {a_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {a_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)$

$= {a_1}{a_2}{b_3} - {a_1}{a_3}{b_2} + {a_2}{a_3}{b_1} - {a_2}{a_1}{b_3} + {a_3}{a_1}{b_2} - {a_3}{a_2}{b_1} = 0$

+) $\vec b.\vec n = {b_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {b_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {b_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)$

$= {b_1}{a_2}{b_3} - {b_1}{a_3}{b_2} + {b_2}{a_3}{b_1} - {b_2}{a_1}{b_3} + {b_3}{a_1}{b_2} - {b_3}{a_2}{b_1} = 0$

Như vậy $\vec a.\vec n = \vec b.\vec n = 0$.

c) Theo câu b, ta có $\vec a.\vec n = \vec b.\vec n = 0$, điều này có nghĩa là $\vec n$ có giá vuông góc với giá của $\vec a$ và $\vec b$. Mà $\vec a$ và $\vec b$ là một cặp vectơ chỉ phương của $\left( \alpha  \right)$, nên $\vec n$ có giá vuông góc với mặt phẳng $\left( \alpha  \right)$. Như vậy $\vec n$ là một vectơ pháp tuyến của $\left( \alpha  \right)$.

TH2

Trả lời câu hỏi Thực hành 2 trang 34 SGK Toán 12 Chân trời sáng tạo

Cho mặt phẳng $\left( Q \right)$ đi qua ba điểm $A\left( {1;1;1} \right)$, $B\left( { - 1;1;5} \right)$, $C\left( {10;7; - 1} \right)$. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của $\left( Q \right)$.

Phương pháp giải:

Mặt phẳng $\left( Q \right)$ đi qua $A\left( {1;1;1} \right)$, $B\left( { - 1;1;5} \right)$, , nên nó sẽ có một cặp vectơ chỉ phương là  và .

Để tìm toạ độ một vectơ pháp tuyến của mặt phẳng , thực hiện tính tích có hướng của hai vectơ  và . Vectơ thu được là một$C\left( {10;7; - 1} \right)$ vectơ pháp tuyến của $\left( Q \right)$.

Lời giải chi tiết:

Ta có $\left( Q \right)$ đi qua $A\left( {1;1;1} \right)$, $B\left( { - 1;1;5} \right)$, $C\left( {10;7; - 1} \right)$, nên nó sẽ có một cặp vectơ chỉ phương là $\overrightarrow {AB} \left( { - 2;0;4} \right)$ và $\overrightarrow {AC} \left( {9;6; - 2} \right)$.

Tích có hướng của hai vectơ $\overrightarrow {AB}$ và $\overrightarrow {AC}$ là:

$\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0.\left( { - 2} \right) - 4.6;4.9 - \left( { - 2} \right).\left( { - 2} \right); - 2.6 - 0.9} \right) = \left( { - 24;32; - 12} \right)$

Do đó, mặt phẳng $\left( Q \right)$ nhận $\vec n = \frac{1}{4}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 6;8; - 3} \right)$ làm một vectơ pháp tuyến.

VD2

Trả lời câu hỏi Vận dụng 2 trang 34 SGK Toán 12 Chân trời sáng tạo

Cho biết hai vectơ $\vec a = \left( {2;1;1} \right)$, $\vec b = \left( {1; - 2;0} \right)$ có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong hình dưới đây. Tìm vectơ $\vec n$ có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành 3 đường thẳng đôi một vuông góc).

Phương pháp giải:

Theo hình vẽ, do vectơ $\vec n$ có giá vuông góc lần lượt với giá của hai vectơ $\vec a$ và $\vec b$, nên có thể chọn vectơ $\vec n$ là tích có hướng của hai vectơ $\vec a$ và $\vec b$.

Lời giải chi tiết:

Theo hình vẽ, do vectơ $\vec n$ có giá vuông góc lần lượt với giá của hai vectơ $\vec a$ và $\vec b$, nên có thể chọn vectơ $\vec n$ là tích có hướng của hai vectơ $\vec a$ và $\vec b$.

Tích có hướng của hai vectơ $\vec a$ và $\vec b$ là

$\left[ {\vec a,\vec b} \right] = \left( {1.0 - 1.\left( { - 2} \right);1.1 - 2.0;2.\left( { - 2} \right) - 1.1} \right) = \left( {2;1; - 5} \right)$.

Do đó, vectơ $\vec n$ cần tìm là $\vec n = \left( {2;1; - 5} \right)$.