Giải mục 2 trang 36, 37 Chuyên đề học tập Toán 12 - Chân trời sáng tạoCông ty A vay của ngân hàng B với hợp đồng vay như sau: Số tiền vay là 100 triệu đồng, thời hạn vay 12 tháng, lãi suất cho vay 9%/năm. Tiền lãi tính theo dư nợ ban đầu. a) Tính tổng số tiền gốc và lãi mà công ty A phải trả cho ngân hàng B vào cuối kì vay. b) Nếu hợp đồng vay yêu cầu tiền gốc phải trả đều mỗi tháng, tiền lãi tính theo dư nợ giảm dần. Tính số tiền gốc và lãi mà công ty A phải trả mỗi tháng và tổng số tiền gốc và lãi công ty đã trả tổng cộng cho hợp đồng vay nói trên.
Lựa chọn câu để xem lời giải nhanh hơn
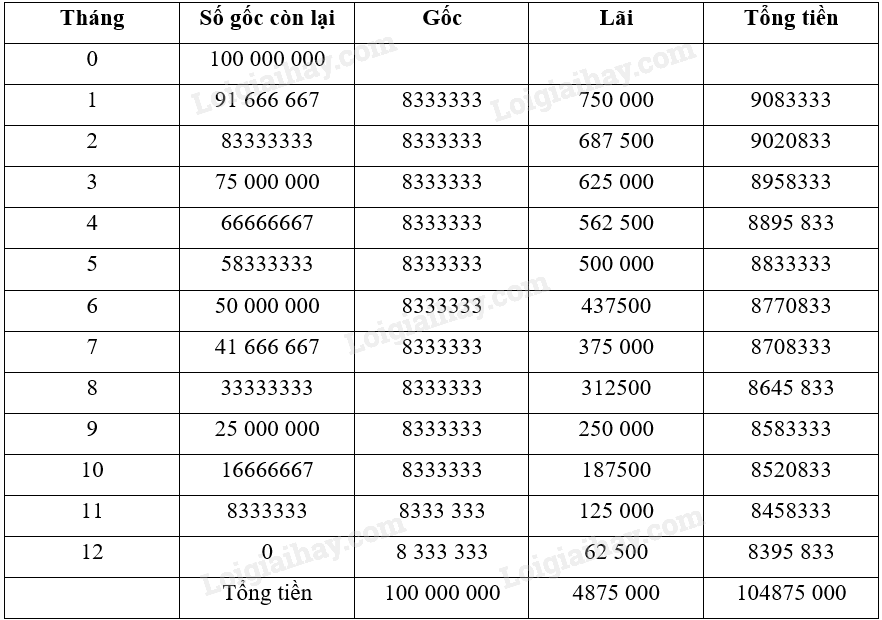
Luyện tập 2 Trả lời câu hỏi Luyện tập 2 trang 37 Chuyên đề học tập Toán 12 Chân trời sáng tạo Công ty A vay của ngân hàng B với hợp đồng vay như sau: Số tiền vay là 100 triệu đồng, thời hạn vay 12 tháng, lãi suất cho vay 9%/năm. Tiền lãi tính theo dư nợ ban đầu. a) Tính tổng số tiền gốc và lãi mà công ty A phải trả cho ngân hàng B vào cuối kì vay. b) Nếu hợp đồng vay yêu cầu tiền gốc phải trả đều mỗi tháng, tiền lãi tính theo dư nợ giảm dần. Tính số tiền gốc và lãi mà công ty A phải trả mỗi tháng và tổng số tiền gốc và lãi công ty đã trả tổng cộng cho hợp đồng vay nói trên. Phương pháp giải: ‒ Lãi đơn: \({I_n} = P.r.n\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn). ‒ Giá trị cả vốn lẫn lãi sau \(n\) chu kì lãi đơn: \({F_n} = P\left( {1 + n{\rm{r}}} \right)\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn). Lời giải chi tiết: a) Do tiền lãi tính theo dư nợ ban đầu nên công ty A sẽ trả nợ ngân hàng B theo phương thức lãi đơn. Ta có: \(P = 100,r = 9\% ,n = 1\). Tổng số tiền gốc và lãi mà công ty A phải trả cho ngân hàng B vào cuối kì vay là: \(100\left( {1 + 9\% } \right) = 109\) (triệu đồng). b) Áp dụng công thức lãi đơn cho từng tháng, theo hợp đồng vay ta có bảng tính sau:
Vận dụng 2 Trả lời câu hỏi Vận dụng 2 trang 37 Chuyên đề học tập Toán 12 Chân trời sáng tạo Bác Hà vay của ngân hàng ABC 500 triệu đồng để mua ô tô với hợp đồng vay như sau: Thời hạn vay 7 năm, gốc trả đều hằng tháng theo số tháng vay, lãi trả hằng tháng với lãi suất 12%/năm tính theo dư nợ giảm dần. Tính: a) Số tiền gốc và lãi mà bác Hà phải trả ở tháng thứ \(k\left( {k = 1,2,...,84} \right)\). b) Tổng số tiền gốc và lãi mà bác Hà phải trả sau 84 tháng. Phương pháp giải: Lãi đơn: \({I_n} = P.r.n\) (với \(P\): vốn gốc, \(r\): lãi suất trên một kì hạn, \(n\): số kì hạn). Lời giải chi tiết: a) Mỗi tháng số tiền gốc phải trả là: \(\frac{{500}}{{84}}\) (triệu đồng). Dư nợ gốc còn lại ở tháng thứ \(k\) là: \(500 - \frac{{500}}{{84}}.\left( {k - 1} \right) = 500.\frac{{85 - k}}{{84}}\) (triệu đồng). Lãi suất trên một tháng là: \(r = \frac{1}{{12}}.12\% = 1\% \) Số tiền lãi phải trả ở tháng thứ \(k\) là: \({I_k} = 500.\frac{{85 - k}}{{84}}.1\% \) (triệu đồng). Số tiền gốc và lãi phải trả ở tháng thứ \(k\) là: \({F_k} = \frac{{500}}{{84}}.k + \left( {85 - k} \right)\frac{{500}}{{84}}.1\% \) (triệu đồng). b) Số tiền gốc phải trả sau 84 tháng là: 500 (triệu đồng). Tổng số tiền lãi phải trả sau 84 tháng là: \(\begin{array}{l}I = 500.\frac{{85 - 1}}{{84}}.1\% + 500.\frac{{85 - 2}}{{84}}.1\% + ... + 500.\frac{{85 - 84}}{{84}}.1\% \\ = 500.\frac{{84}}{{84}}.1\% + 500.\frac{{83}}{{84}}.1\% + ... + 500.\frac{1}{{84}}.1\% \end{array}\) \( = \frac{{500}}{{84}}.1\% \left( {1 + 2 + ... + 84} \right) = \frac{{500}}{{84}}.1\% .\frac{{84\left( {1 + 84} \right)}}{2} = 212,5\) (triệu đồng). Tổng số tiền gốc và lãi bác Năm phải trả sau 84 tháng là \(500 + 212,5 = 712,5\) (triệu đồng).
|