Giải mục 3 trang 29, 30, 31, 32 Chuyên đề học tập Toán 12 - Kết nối tri thứcXét bài toán quy hoạch tuyến tính F(x; y) = 3x + 4y → min với các ràng buộc (left{ begin{array}{l}x ge 0,y ge 0\x + 2y ge 4\x + y ge 3end{array} right.) a) Kiểm tra lại rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán. b) Tìm tập hợp các điểm M(x; y) thoả mãn F(x; y) = 3x + 4y = 12. c) Với mỗi số thực m, xét đường thẳng dm: 3x + 4y = m. Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅. d) Từ phần c suy ra giá trị nhỏ nhất của F(x; y) trên miền chấp nhận
Lựa chọn câu để xem lời giải nhanh hơn
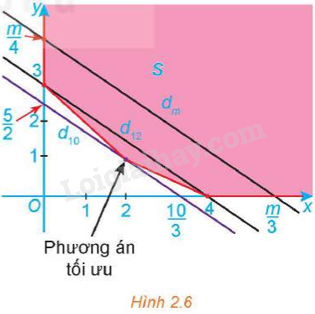
Hoạt động 3 Trả lời câu hỏi Hoạt động 3 trang 29 Chuyên đề học tập Toán 12 Kết nối tri thức Xét bài toán quy hoạch tuyến tính F(x; y) = 3x + 4y → min với các ràng buộc \(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\x + 2y \ge 4\\x + y \ge 3\end{array} \right.\) a) Kiểm tra lại rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán.
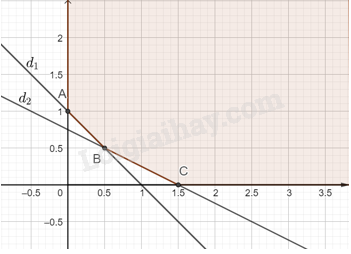
b) Tìm tập hợp các điểm M(x; y) thoả mãn F(x; y) = 3x + 4y = 12. c) Với mỗi số thực m, xét đường thẳng dm: 3x + 4y = m. Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅. d) Từ phần c suy ra giá trị nhỏ nhất của F(x; y) trên miền chấp nhận được. Chứng tỏ rằng, giá trị nhỏ nhất này chính là giá trị của F(x; y) tại một điểm cực biên của miền chấp nhận được. Phương pháp giải: Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được. Lời giải chi tiết: a) Ta thấy rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán. b) Theo bài, F(x; y) = 3x + 4y = 12. Vậy tập hợp điểm M(x; y) thỏa mãn yêu cầu đề bài là tập hợp các điểm nằm trên đường thẳng d: 3x + 4y = 12 nằm trong miền S. b) Vì đường thẳng dm song song với đường thẳng (d) nên đường thẳng dm: 3x + 4y = m luôn cắt trục tung tại điểm có tung độ \(y = \frac{m}{4}\). Để dm ∩ S ≠ ∅ thì \(\frac{m}{4} \ge \frac{5}{2}\) hay m ≥ 10. Vậy m ≥ 10. c) Ta có: F(x; y) = 3x + 4y = m, mà theo kết quả của câu b, ta có m ≥ 10 nên F(x; y) ≥ 10. Vậy giá trị nhỏ nhất của F(x; y) trên miền S là 10. Ta có các điểm cực biên của miền S là: (0; 3), (2; 1), (4; 0). ⦁ F(0; 3) = 3.0 + 4.3 = 12; ⦁ F(2; 1) = 3.2 + 4.1 = 10; ⦁ F(4; 0) = 3.4 + 4.0 = 12. Vậy giá trị nhỏ nhất của F(x; y) trên miền S chính là giá trị của F(x; y) tại điểm cực biên có tọa độ (2; 1) của miền chấp nhận được. Luyện tập 3 Trả lời câu hỏi Luyện tập 3 trang 32 Chuyên đề học tập Toán 12 Kết nối tri thức Giải bài toán quy hoạch tuyến tính sau: F(x; y) = x + 2y → min với các ràng buộc \(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\x + y \ge 1\\2{\rm{x}} + 4y \ge 3\end{array} \right.\) Phương pháp giải: Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được. Lời giải chi tiết: Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:
Có ba điểm cực biên là A(0; 1), B(0,5; 0,5), C(1,5; 0). Ta có: F(0; 1) = 2. F(0,5; 0,5) = 1,5. F(1,5; 0) = 1,5. Vậy hệ có hai nghiệm thỏa mãn là B(0,5; 0,5) và C(1,5; 0). Vận dụng Trả lời câu hỏi Vận dụng trang 32 Chuyên đề học tập Toán 12 Kết nối tri thức Một chủ trang trại cần sử dụng phân bón để chăm sóc cho một loại đậu tương. Loại đậu tương này cần ít nhất 18 đơn vị đạm và ít nhất 6 đơn vị phosphate. Ông chủ trang trại có thể sử dụng hai loại phân bón X và Y. Giá cả, hàm lượng đạm và hàm lượng phosphate có trong một tạ phân X và một tạ phân Y được cho bởi bảng sau:
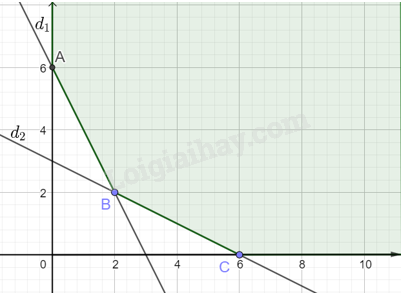
Hãy cho biết cần phải mua bao nhiêu tạ phân loại X, bao nhiêu tạ phân loại Y để chi phí là thấp nhất mà vẫn đảm bảo chế độ dinh dưỡng cho loại đậu tương trên? Phương pháp giải: Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được. Lời giải chi tiết: Gọi x, y lần lượt là số tạ phân bón loại X là Y cần phải mua. Chi phí mua phân bón là: F(x; y) = 1,7x + 1,2y (triệu đồng). Hệ bất phương trình ràng buộc x và y là \(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\3x + 6y \ge 18\\2x + y \ge 6\end{array} \right.\) Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:
Các điểm cực biên là: A(0; 6), B(2; 2), C(6; 0). Ta có: F(0; 6) = 1,7.0 + 1,2.6 = 7,2 F(2; 2) = 1,7.2 + 1,2.2 = 5,8 F(6; 0) = 1,7.6 + 1,2.0 = 10,2 Do đó giá trị nhỏ nhất của F(x; y) bằng 5,8 triệu đồng tại điểm B(2; 2). Vậy cần phải mua 2 tạ phân bón loại X và 2 tạ phân bón loại Y để chi phí là thấp nhất mà vẫn đảm bảo chế độ dinh dưỡng cho loại đậu tương trên.
|