Giải mục 3 trang 68, 69, 70 SGK Toán 10 tập 2 - Chân trời sáng tạo

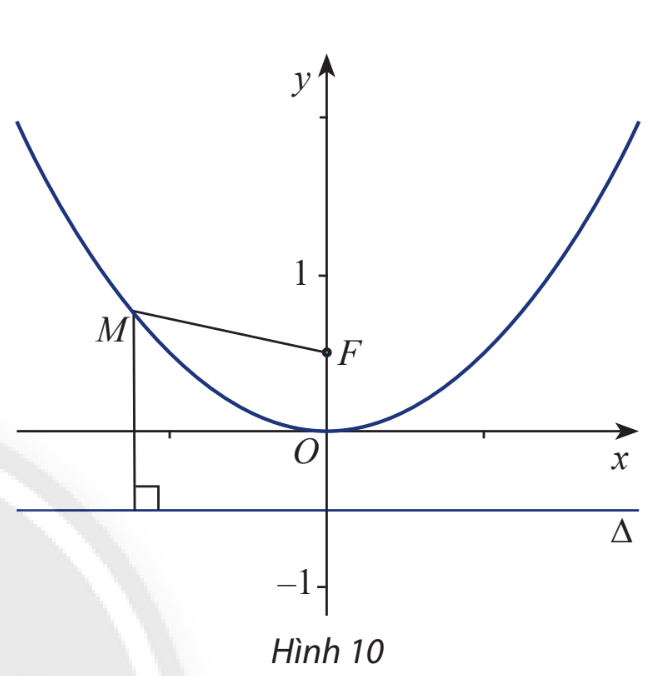
HĐ Khám phá 5

Trong mặt phẳng Oxy, cho điểm $F\left( {0;\frac{1}{2}} \right)$, đường thẳng $\Delta :y + \frac{1}{2} = 0$ và điểm $M(x;y)$. Để tìm hệ thức giữa x và y sao cho $M$ cách đều  F và $\Delta$, một học sinh đã làm như sau:

+) Tính MF và MH (với H là hình chiếu của M trên $\Delta$):

$MF = \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} ,MH = d\left( {M,\Delta } \right) = \left| {y + \frac{1}{2}} \right|$

+) Điều kiện để M cách đều F  và $\Delta$:

$\begin{array}{l}MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}}  = \left| {y + \frac{1}{2}} \right|\\ \Leftrightarrow {x^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {y + \frac{1}{2}} \right)^2}\\ \Leftrightarrow {x^2} = 2y \Leftrightarrow y = \frac{1}{2}{x^2}\left( * \right)\end{array}$

Hãy cho biết tên đồ thị (P) của hàm số (*) vừa tìm được.

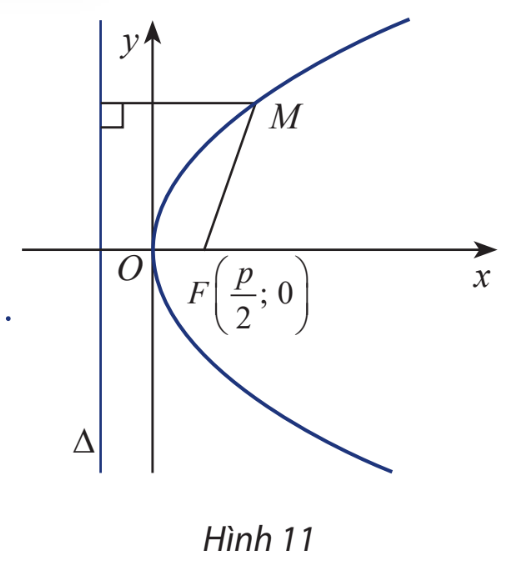
Lời giải chi tiết:

Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.

HĐ Khám phá 6

Cho parabol (P) có tiêu điểm F  và đường chuẩn $\Delta$. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên $p > 0$.

Chọn hệ trục tọa độ Oxy sao cho $F\left( {\frac{p}{2};0} \right)$ và $\Delta :x + \frac{p}{2} = 0$.

Xét điểm $M(x;y)$.

a) Tính MF và $d\left( {M,\Delta } \right)$.

b) Giải thích biểu thức sau:

$M(x;y) \in (P) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}}  = \left| {x + \frac{p}{2}} \right|$.

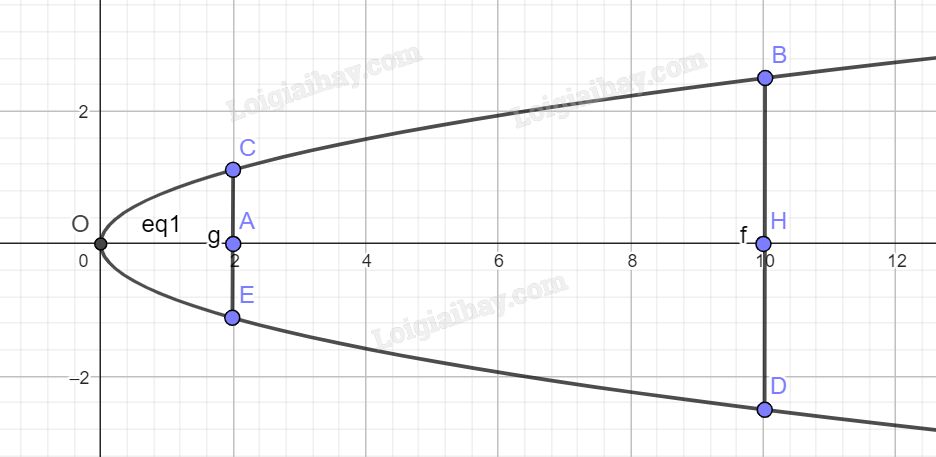
Phương pháp giải:

Sử dụng phương pháp tọa độ trong mặt phẳng.

Lời giải chi tiết:

a) Ta có: $\overrightarrow {FM}  = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}}$.

$d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|$.

b) M thuộc parabol (P) nên M cách đều F và $\Delta$.

Suy ra $MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}}  = \left| {x - \frac{p}{2}} \right|$.

Thực hành 3

Viết phương trình chính tắc của parabol (P) có đường chuẩn $\Delta :x + 1 = 0$.

Phương pháp giải:

Bước 1: Từ phương trình đường chuẩn tìm tọa độ của tiêu điểm (phương trình đường chuẩn có dạng $x + \frac{p}{2} = 0$.

Bước 2: Viết phương trình chính tắc của parabol có dạng ${y^2} = 2px$ với $M(x;y) \in (P)$.

Lời giải chi tiết:

Từ phương trình đường chuẩn $\Delta :x + 1 = 0$ ta có tiêu điểm $F\left( {1;0} \right)$.

Phương trình chính tắc của parabol có dạng ${y^2} = 2x$.

Vận dụng 3

Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.

Phương pháp giải:

Bước 1: Gọi phương trình của parabol một cách tổng quát.

Bước 2: Thay các giả thiết tìm tiêu điểm.

Bước 3: Thay $x = 2$ vào phương trình chính tắc tìm y.

Lời giải chi tiết:

Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới.

Gọi phương trình của parabol là ${y^2} = 2px$.

Ta có chiều cao của cổng $OH = 10$, chiều rộng tại chân cổng $BD = 2BH = 5$.

Vậy điểm B có tọa độ là $B\left( {10;\frac{5}{2}} \right)$.

Thay tọa độ điểm B vào phương trình parabol ta có:

${\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}$, suy ra phương trình parabol có dạng ${y^2} = \frac{5}{8}x$.

Thay $x = 2$ vào phương trình ${y^2} = \frac{5}{8}x$ ta tìm được $y = CA = \frac{{\sqrt 5 }}{2}$.

Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là $\sqrt 5$ m.