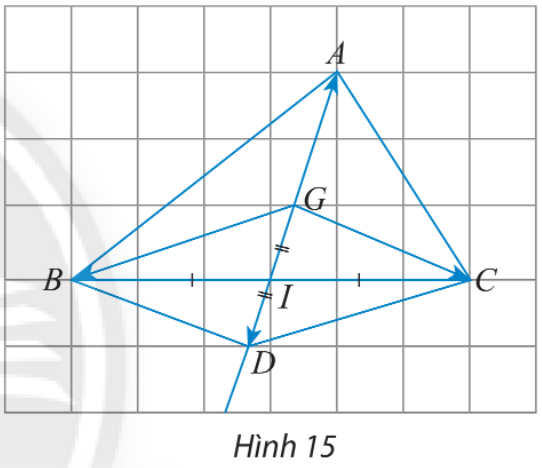
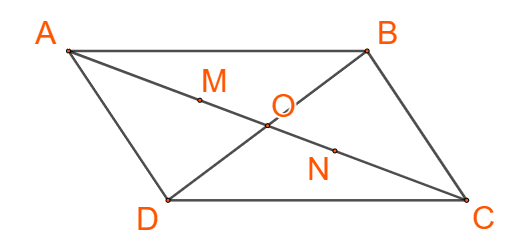
Giải mục 4 trang 92, 93 SGK Toán 10 tập 1 - Chân trời sáng tạo

HĐ Khám phá 4

a) Cho điểm M là trung điểm của đoạn thẳng AB. Ta đã biết $\overrightarrow {MB}  =  - \overrightarrow {MA}  = \overrightarrow {AM} .$ Hoàn thành phép cộng vectơ sau: $\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow {MA}  + \overrightarrow {AM}  = \overrightarrow {MM}  = ?$

b) Cho điểm G là trọng tâm của tam giác ABC có trung tuyến AI. Lấy D là điểm đối xứng với G qua I. Ta có BGCD là hình bình hành và G là trung điểm của đoạn thẳng AD. Với lưu ý rằng $\overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow {GD}$ và $\overrightarrow {GA}  = \overrightarrow {DG}$, hoàn thành các phép cộng vectơ sau:

$\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow {GA}  + \overrightarrow {GD}  = \overrightarrow {{\rm{DD}}}  = ?$

Phương pháp giải:

a) Thay thế các vectơ bằng nhau $\overrightarrow {MB}  =  - \overrightarrow {MA}  = \overrightarrow {AM} .$

b) Bước 1: Áp dụng quy tắc hình bình hành trên BGCD

Bước 2: Áp dụng tính chất trung điểm vừa tìm được ở câu a) $\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0$

(với M là trung điểm của AB)

Lời giải chi tiết:

a) $\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow {MA}  + \overrightarrow {AM}  = \overrightarrow {MM}  = \overrightarrow 0$ (vì vectơ $\overrightarrow {MB}  =  - \overrightarrow {MA}  = \overrightarrow {AM} .$)

b) Xét hình bình hành BGCD ta có: $\overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow {GD}$

$\Rightarrow \overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow {GA}  + \overrightarrow {GD}  = \overrightarrow {DG}  + \overrightarrow {GD}  = \overrightarrow {{\rm{DD}}}  = \overrightarrow 0$

(vì $\overrightarrow {GA}  =  - \overrightarrow {GD}  = \overrightarrow {DG}$)

Thực hành 5

Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:

a) $\overrightarrow {MA}  + \overrightarrow {MD}  + \overrightarrow {MB}  = \overrightarrow 0$ 

b) $\overrightarrow {ND}  + \overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0$     

c) $\overrightarrow {PM}  + \overrightarrow {PN}  = \overrightarrow 0$

Phương pháp

a)  Sử dụng tính chất trọng tâm của tam giác $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0$(với G là trọng tâm của tam giác ABC)

b) Sử dụng tính chất trọng tâm của tam giác $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0$

c) Sử dụng tính chất trung điểm $\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0$(với M là trung điểm của AB)

Phương pháp giải:

a) Sử dụng tính chất trọng tâm của tam giác $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0$(với G là trọng tâm của tam giác ABC)

b) Sử dụng tính chất trọng tâm của tam giác $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0$

c) Sử dụng tính chất trung điểm $\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0$(với M là trung điểm của AB)

Lời giải chi tiết:

a) Áp dụng tính chất trọng tâm ta có: $\overrightarrow {MA}  + \overrightarrow {MD}  + \overrightarrow {MB}  = \overrightarrow 0$

Suy ra M là trọng tâm của tam giác ADB

Vậy M nằm trên đoạn thẳng AO sao cho $AM = \frac{2}{3}AO$

b) Tiếp tục áp dụng tính chất trọng tâm $\overrightarrow {ND}  + \overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0$

Suy ra N là trọng tâm của tam giác BCD

Vậy N nằm trên đoạn thẳng OD sao cho $ON = \frac{1}{3}OD$

c) Áp dụng tính chất trung điểm ta có: $\overrightarrow {PM}  + \overrightarrow {PN}  = \overrightarrow 0$

Suy ra P là trung điểm của đoạn thẳng MN

Vậy điểm P trùng với điểm O