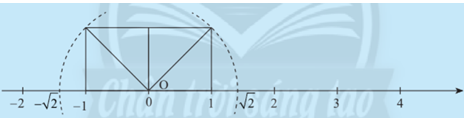
Giải mục 5 trang 37 SGK Toán 7 tập 1 - Chân trời sáng tạoTrên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm....Tìm giá trị tuyệt đối của các số thực sau: -3,14; 41; -5; 1,(2); -5...Có bao nhiêu số thực x thoả mãn |x| = căn 3 Video hướng dẫn giải HĐ 5 Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm √2√2 và −√2−√2.
Phương pháp giải: Quan sát hình vẽ và so sánh khoảng cách từ 0 đến hai điểm √2√2 và −√2−√2. Lời giải chi tiết: Ta thấy khoảng cách từ 0 đến điểm √2√2 bằng √2√2. Khoảng cách từ 0 đến điểm -√2√2 bằng √2√2 Vậy khoảng cách từ 0 đến hai điểm √2√2 và −√2−√2 bằng nhau. Thực hành 5 Tìm giá trị tuyệt đối của các số thực sau: −3,14;41;−5;1,(2);−√5−3,14;41;−5;1,(2);−√5. Phương pháp giải: |x|=x nếu x>0 |x|=-x nếu x<0 |x|=0 nếu x=0 Lời giải chi tiết: |−3,14|=3,14;|41|=41;|−5|=5;|1,(2)|=1,(2);|−√5|=√5.|−3,14|=3,14;|41|=41;|−5|=5;|1,(2)|=1,(2);∣∣−√5∣∣=√5. Vận dụng 4 Có bao nhiêu số thực x thoả mãn |x| = √3√3? Phương pháp giải: Giá trị tuyệt đối của một số thực âm hoặc dương đều là một số hữu tỉ dương. Lời giải chi tiết: Có hai số thực x thỏa mãn là: x=√3;x=−√3x=√3;x=−√3.  Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
