Giải mục I trang 93, 94 SGK Toán 10 tập 1 - Cánh diềuCho tam giác ABC đều cạnh a, AH là đường cao. Tính:
Lựa chọn câu để xem lời giải nhanh hơn
LT-VD 1 Cho tam giác ABC vuông tại A có \(\widehat B = {30^o},AB = 3\;cm.\) Tính \(\overrightarrow {BA} .\overrightarrow {BC} ;\;\overrightarrow {CA} .\overrightarrow {CB} .\) Phương pháp giải: +) Tính tích vô hướng \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng công thức \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} )\) Trong đó: \((\overrightarrow {BA} ,\overrightarrow {BC} ) = \widehat {ABC}\) là góc giữa hai vecto \(\overrightarrow {BA} ,\overrightarrow {BC} \) Lời giải chi tiết:
Ta có: \(BC = \frac{{AB}}{{\cos {{30}^o}}} = 3:\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \); \(AC = BC.\sin \widehat {ABC} = 2\sqrt 3 .\sin {30^o} = \sqrt 3 .\) \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = 3.2\sqrt 3 .\cos \widehat {ABC} = 6\sqrt 3 .\cos {30^o} = 6\sqrt 3 .\frac{{\sqrt 3 }}{2} = 9.\) \(\overrightarrow {CA} .\overrightarrow {CB} = \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|\cos (\overrightarrow {CA} ,\overrightarrow {CB} ) = \sqrt 3 .2\sqrt 3 .\cos \widehat {ACB} = 6.\cos {60^o} = 6.\frac{1}{2} = 3.\) LT-VD 2 Cho tam giác ABC đều cạnh a, AH là đường cao. Tính: a) \(\overrightarrow {CB} .\overrightarrow {BA} \) b) \(\overrightarrow {AH} .\overrightarrow {BC} \) Phương pháp giải: +) Tính tích vô hướng \(\overrightarrow {CB} .\overrightarrow {BA} \) bằng công thức \(\overrightarrow {CB} .\overrightarrow {BA} = \left| {\overrightarrow {CB} } \right|.\left| {\overrightarrow {BA} } \right|\cos (\overrightarrow {CB} ,\overrightarrow {BA} )\) +) \((\overrightarrow {CB} ,\overrightarrow {BA} ) = (\overrightarrow {BD} ,\overrightarrow {BA} )\) nếu \(\overrightarrow {BD} = \overrightarrow {CB} \) Lời giải chi tiết:
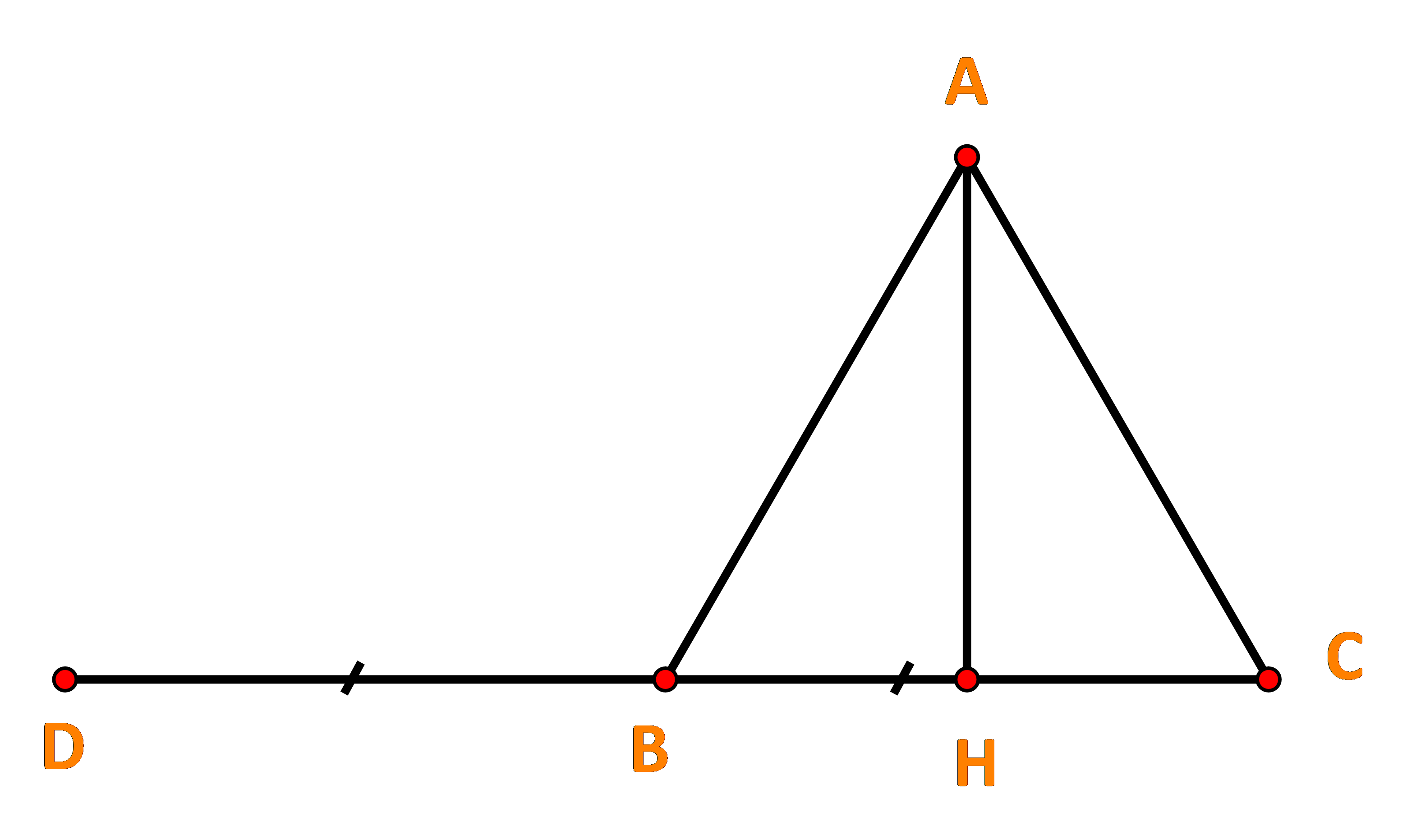
a) Vẽ vecto \(\overrightarrow {BD} = \overrightarrow {CB} \). Ta có: \((\overrightarrow {CB} ,\overrightarrow {BA} ) = (\overrightarrow {BD} ,\overrightarrow {BA} ) = \widehat {DBA} = {120^o}\) Vậy \(\overrightarrow {CB} .\overrightarrow {BA} = \left| {\overrightarrow {CB} } \right|.\left| {\overrightarrow {BA} } \right|\cos (\overrightarrow {CB} ,\overrightarrow {BA} ) = a.a.\cos {120^o} = {a^2}.\left( { - \frac{1}{2}} \right) = - \frac{{{a^2}}}{2}.\) b) Vì \(AH \bot BC\) nên \[(\overrightarrow {AH} ,\overrightarrow {BC} ) = {90^o}\], suy ra \(\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = \cos {90^o} = 0.\) Vậy \(\overrightarrow {AH} .\overrightarrow {BC} = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = 0.\)
|