Giải mục II trang 27, 28, 29 SGK Vật Lí 10 - Kết nối tri thứcMột người đi xe máy đi từ ngã tư (Hình 5.1) với tốc độ trung bình 30 km/h theo hướng Bắc. Sau 3 phút người đó đến vị trí nào trên hình. Theo em, biểu thức nào sau đây xác định giá trị vận tốc. Tại sao. Bạn A đi học từ nhà đến trường theo lộ trình ABC (Hình 5.2). Biết bạn A đi đoạn đường AB = 400 m hết 6 phút, đoạn đường BC = 300 m hết 4 phút. Một con kiến bò quanh miệng của một cái chén được 1 vòng hết 3 giây. Bán kính của miệng chén là 3 cm. Hãy xác định vận tốc của hành khách đối với mặt đường
Lựa chọn câu để xem lời giải nhanh hơn
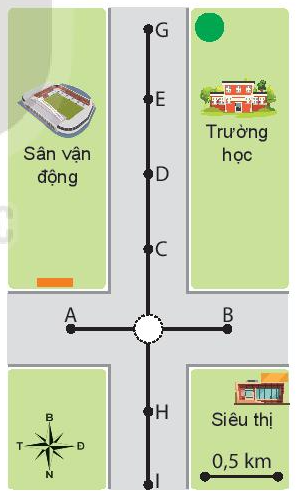
Câu hỏi 1 Giải câu hỏi 1 trang 27 SGK Vật Lí 10 Một người đi xe máy đi từ ngã tư (Hình 5.1) với tốc độ trung bình 30 km/h theo hướng Bắc. Sau 3 phút người đó đến vị trí nào trên hình?
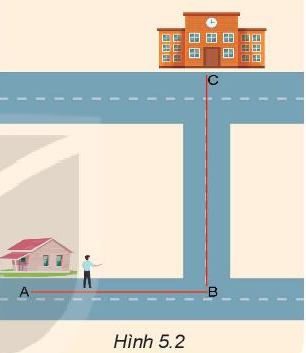
Phương pháp giải: Sử dụng công thức: \(v = \frac{s}{t}\) Lời giải chi tiết: Đổi: 3 phút = 0,05 giờ Quãng đường người đó đi được sau 3 phút là: Ta có: \(v = \frac{s}{t} \Rightarrow s = v.t = 30.0,05 = 1,5\left( {km} \right)\) Vậy sau 3 phút, người đó đến vị trí E trên hình. Câu hỏi 2 Giải câu hỏi 2 trang 27 SGK Vật Lí 10 Theo em, biểu thức nào sau đây xác định giá trị vận tốc? Tại sao? a) \(\frac{s}{t}\) b) \(vt\) c) \(\frac{d}{t}\) d) \(d.t\) Lời giải chi tiết: Biểu thức xác định giá trị vận tốc là biểu thức : c) \(\frac{d}{t}\) Vì d là độ dịch chuyển của vật sẽ cho chúng ta biết được độ dịch chuyển của vật trong một đơn vị thời gian xác định. Câu hỏi 3 Giải câu hỏi 3 trang 28 SGK Vật Lí 10 1. Bạn A đi học từ nhà đến trường theo lộ trình ABC (Hình 5.2). Biết bạn A đi đoạn đường AB = 400 m hết 6 phút, đoạn đường BC = 300 m hết 4 phút. Xác định tốc độ trung bình và vận tốc trung bình của bạn A khi đi từ nhà đến trường.
2. Một con kiến bò quanh miệng của một cái chén được 1 vòng hết 3 giây. Bán kính của miệng chén là 3 cm. a) Tính quãng đường đi được và độ dịch chuyển của kiến. b) Tính tốc độ trung bình và vận tốc trung bình của con kiến ra cm/s. Phương pháp giải: 1. - Xác định độ dài quãng đường từ nhà đến trường - Xác định thời gian từ nhà đến trường - Xác định độ dịch chuyển từ nhà đến trường - Sử dụng công thức tính tốc độ trung bình và vận tốc trung bình. 2. - Tính độ dài 1 vòng tròn (chu vi hình tròn) - Sử dụng công thức tính tốc độ trung bình và vận tốc trung bình. Lời giải chi tiết: 1. - Độ dài quãng đường từ nhà đến trường là: \(s = AB + BC = 400 + 300 = 700\left( m \right)\) - Thời gian đi từ nhà đến trường là: \(t = 6 + 4 = 10\) (phút) - Tốc độ trung bình của bạn A khi đi từ nhà đến trường là: \(v = \frac{s}{t} = \frac{{700}}{{10}} = 70\left( {m/ph} \right)\) - Độ dịch chuyển của bạn A là: \(d = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{400}^2} + {{300}^2}} = 500\left( m \right)\) - Vận tốc trung bình của bạn A khi đi từ nhà đến trường là: \(v = \frac{d}{t} = \frac{{500}}{{6 + 4}} = 50\left( {m/ph} \right)\) 2. a) - Quãng đường đi được của con kiến là: \(s = 2\pi r = 2\pi .0,03 = 0,06\pi = 0,1884m = 18,84\left( {cm} \right)\) - Con kiến bò quanh miệng cốc, không đổi chiều chuyển động nên độ dịch chuyển và quãng đường đi được bằng nhau: \(d = s = 18,84\left( {cm} \right)\) b) Tốc độ trung bình của con kiến là: \(v = \frac{s}{t} = \frac{{18,84}}{3} = 6,28\left( {cm/s} \right)\) Do \(d = s\) nên vận tốc trung bình bằng tốc độ trung bình và bằng 6,28 cm/s. Câu hỏi 4 Giải câu hỏi 4 trang 28 SGK Vật Lí 10 1. Hãy xác định vận tốc của hành khách đối với mặt đường nếu người này chuyển động về cuối đoàn tàu với vận tốc có cùng độ lớn 1 m/s. 2. Một người bơi trong bể bơi yên lặng có thể đạt tới vận tốc 1 m/s. Nếu người này bơi xuôi dòng sông có dòng chảy với vận tốc 1 m/s thì có thể đạt vận tốc tối đa là bao nhiêu? 3. Một canô chạy hết tốc lực trên mặt nước yên lặng có thể đạt 21,5 km/h. Canô này chạy xuôi dòng sông trong 1 giờ rồi quay lại thì phải mất 2 giờ nữa mới về tới vị trí ban đầu. Hãy tính vận tốc chảy của dòng sông. Phương pháp giải: Sử dụng công thức tổng hợp vận tốc. Lời giải chi tiết: 1. Đổi: 36 km/h = 10 m/s Gọi: \({\overrightarrow v _{1,2}}\) là vận tốc của hành khách so với tàu \({\overrightarrow v _{2,3}}\) là vận tốc của tàu so với mặt đường \({\overrightarrow v _{1,3}}\) là vận tốc của hành khách so với mặt đường Suy ra, ta có: \({\overrightarrow v _{1,3}} = {\overrightarrow v _{1,2}} + {\overrightarrow v _{2,3}}\) Do hành khách chuyển động về cuối đoàn tàu, tức là ngược chiều chuyển động của đoàn tàu nên ta có: \({v_{1,3}} = - {v_{1,2}} + {v_{2,3}} = - 1 + 10 = 9\left( {m/s} \right)\) Vậy vận tốc của hành khách đối với mặt đường trong trường hợp này là 9 m/s. 2. Gọi: \({\overrightarrow v _{1,2}}\) là vận tốc của người so với nước \({\overrightarrow v _{2,3}}\) là vận tốc của nước so với bờ \({\overrightarrow v _{1,3}}\) là vận tốc của người so với bờ Ta có: \({\overrightarrow v _{1,3}} = {\overrightarrow v _{1,2}} + {\overrightarrow v _{2,3}}\) - Khi người bơi trong bể nước yên lặng, tức \({v_{2,3}} = 0\), ta có: \({v_{1,2}} = {v_{1,3}} = 1\left( {m/s} \right)\) - Khi người này bơi xuôi dòng chảy với vận tốc \({v_{2,3}} = 1\left( {m/s} \right)\), ta có: \({v_{1,3}} = {v_{1,2}} + {v_{2,3}} = 1 + 1 = 2\left( {m/s} \right)\) Vậy nếu người này bơi xuôi dòng sông có dòng chảy với vận tốc 1 m/s thì có thể đạt vận tốc tối đa là 2 m/s. 3. Gọi: \({\overrightarrow v _{1,2}}\) là vận tốc của canô so với nước \({\overrightarrow v _{2,3}}\) là vận tốc của nước so với bờ \({\overrightarrow v _{1,3}}\) là vận tốc của canô so với bờ Ta có: \({\overrightarrow v _{1,3}} = {\overrightarrow v _{1,2}} + {\overrightarrow v _{2,3}}\) - Khi canô chạy trên mặt nước yên lặng, tức \({v_{2,3}} = 0\), ta có: \({v_{1,2}} = {v_{1,3}} = 21,5\left( {km/h} \right)\) - Khi canô chạy xuôi dòng sông, ta có: \(v{'_{1,3}} = {v_{1,2}} + {v_{2,3}} = 21,5 + {v_{2,3}}\) \( \Rightarrow {t_1} = \frac{d}{{21,5 + {v_{2,3}}}} \Leftrightarrow 1 = \frac{d}{{21,5 + {v_{2,3}}}} \Leftrightarrow 21,5 = d - {v_{2,3}}\) (1) - Khi canô quay lại, ta có: \(v{'_{1,3}} = {v_{1,2}} - {v_{2,3}} = 21,5 - {v_{2,3}}\) \( \Rightarrow {t_1} = \frac{d}{{21,5 - {v_{2,3}}}} \Leftrightarrow 2 = \frac{d}{{21,5 - {v_{2,3}}}} \Leftrightarrow 43 = d + 2{v_{2,3}}\) (2) - Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}d = 28,67\left( {km} \right)\\{v_{2,3}} = 7,17\left( {km/h} \right)\end{array} \right.\) Vậy vận tốc chảy của dòng sông là 7,17 km/h. Câu hỏi 5 Giải câu hỏi 5 trang 29 SGK Vật Lí 10 1. Một máy bay đang bay theo hướng Bắc với vận tốc 200 m/s thì bị gió từ hướng Tây thổi vào với vận tốc 20 m/s. Xác định vận tốc tổng hợp của máy bay lúc này. 2. Một người lái máy bay thể thao đang tập bay ngang. Khi bay từ A đến B thì vận tốc tổng hợp của máy bay là 15 m/s theo hướng 600 Đông – Bắc và vận tốc của gió là 7,5 m/s theo hướng Bắc. a) Hãy chứng minh rằng khi bay từ A đến B thì người lái phải luôn hướng máy bay về hướng Đông. b) Sau khi bay 5 km từ A đến B, máy bay quay lại theo đường BA với vận tốc tổng hợp 13,5 m/s. Coi thời gian ở lại B là không đáng kể, tính tốc độ trung bình trên cả tuyến đường từ A đến B rồi trở lại A. Phương pháp giải: - Sử dụng lý thuyết tổng hợp hai vận tốc vuông góc với nhau. - Sử dụng công thức tính tốc độ trung bình. Lời giải chi tiết: 1. Gọi: \({\overrightarrow v _{1,2}}\) là vận tốc của máy bay so với gió \({\overrightarrow v _{2,3}}\) là vận tốc của gió so với đường bay \({\overrightarrow v _{1,3}}\) là vận tốc của máy bay so với đường bay Suy ra: Vận tốc tổng hợp của máy bay lúc này là: \({v_{1,3}} = \sqrt {v_{1,2}^2 + v_{2,3}^2} = \sqrt {{{200}^2} + {{20}^2}} = 201\left( {m/s} \right)\) 2. a)
b) Quãng đường máy bay đã đi là: \(s = 2AB = 2.5 = 10km\) Thời gian máy bay, bay từ A đến B là: \({t_1} = \frac{{AB}}{{{v_1}}} = \frac{{5000}}{{15}} = 333\left( s \right)\) Thời gian máy bay, bay từ B về A là: \({t_2} = \frac{{BA}}{{13,5}} = \frac{{5000}}{{13,5}} = 370\left( s \right)\) Tốc độ trung bình trên cả tuyến đường bay là: \(v = \frac{s}{{{t_1} + {t_2}}} = \frac{{10000}}{{333 + 370}} = 14,2\left( {m/s} \right)\)
|