Hình vuông có tính chất gì? Đường chéo của hình vuông có đặc điểm gì? - Toán 8

Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.

+ Hình vuông là hình thoi có một góc vuông.

Như vậy, hình vuông vừa là hình chữ nhật, vừa là hình thoi.

Ví dụ:

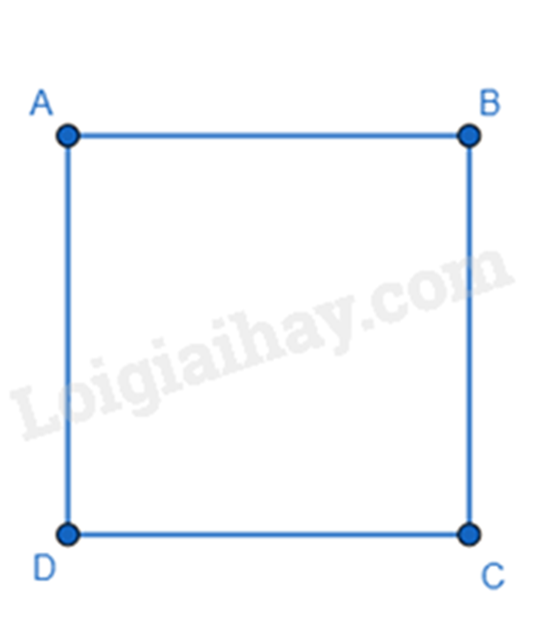
Cho ABCD là hình vuông, khi đó:

+ Bốn cạnh bằng nhau: AB = BC = CD = DA

+ Bốn góc bằng nhau và bằng \(90^\circ \): \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \).

- Trong một hình vuông

+ Các cạnh đối song song.

+ Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

+ Hai đường chéo là các đường phân giác của các góc ở đỉnh (mỗi góc có số đo bằng \(45^\circ \))

- Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

Ví dụ:

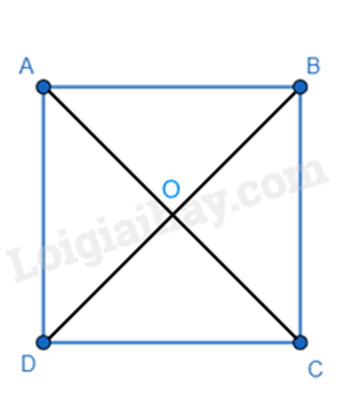
Xét hình vuông ABCD có \(O\) là giao điểm của hai đường chéo, ta có:

+  Bốn cạnh bằng nhau: \(AB = BC = CD = DA\).

+  Bốn góc vuông: \(\hat A = \hat B = \hat C = \hat D = 90^\circ \).

+  Các cạnh đối song song: \(AB\parallel CD\) và \(AD\parallel BC\).

+  Hai đường chéo bằng nhau và vuông góc với nhau: \(AC = BD\) và \(AC \bot BD\).

+  Hai đường chéo cắt nhau tại trung điểm của mỗi đường: \(OA = OB = OC = OD\).

+  Hai đường chéo là các đường phân giác của các góc ở đỉnh:

\(\widehat {ABD} = \widehat {ADB} = \widehat {CBD} = \widehat {CDB} = \widehat {BAC} = \widehat {BCA} = \widehat {DAC} = \widehat {DCA} = 45^\circ \).

Trong hình chữ nhật,

+ Hai cạnh đối song song và bằng nhau

+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

+ Hình chữ nhật có tất cả tính chất của hình thang và hình bình hành.

Ví dụ:

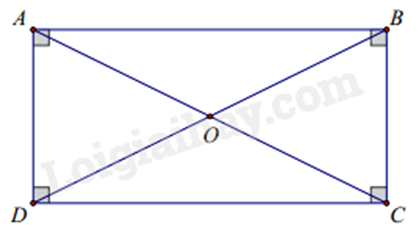
Hình chữ nhật ABCD có O là giao điểm của hai đường chéo, ta có:

+ AB // CD và AB = CD.

+ AD // BC và AD = BC.

+ AC = BD và OA = OB = OC = OD.

Trong hình thoi:

+ Các cạnh đối song song;

+ Các góc đối bằng nhau;

+ Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;

+ Hai đường chéo là các đường phân giác của các góc ở đỉnh.

+ Hình thoi có đầy đủ tính chất của hình bình hành.

Ví dụ:

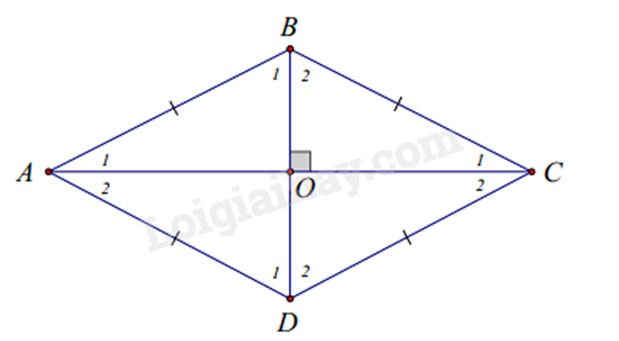
Xét hình thoi ABCD có \(O\) là giao điểm hai đường chéo, ta có:

+ Các cạnh đối song song: \(AB\parallel BC\) và \(BC\parallel DA\).

+ Các góc đối bằng nhau: \(\hat A = \hat B\) và \(\hat B = \hat D\).

+  Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường: \(AC \bot BD\) và \(OA = OC;OB = OD\).

+ Hai đường chéo là các đường phân giác của các góc ở đỉnh: \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{C_1}} = \widehat {{C_2}}\) và \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\).

Đường chéo của hình vuông:

+ bằng nhau

+ vừa vuông góc với nhau

+ cắt nhau tại trung điểm của mỗi đường

+ là các đường phân giác của các góc của hình vuông.