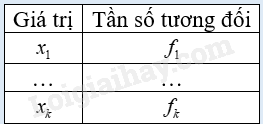
Lý thuyết Bảng tần số tương đối và biểu đồ tần số tương đối Toán 9 Kết nối tri thức1. Bảng tần số tương đối Cho dãy dữ liệu \({x_1},{x_2},...,{x_n}\). Tần số tương đối \({t_i}\) của giá trị \({x_i}\) là tỉ số giữa tần số của \({x_i}\) (gọi là \({m_i}\)) với n. 1. Bảng tần số tương đối
Ví dụ: Cho bảng thống kê số anh, chị, em ruột của các bạn trong lớp:
Tổng số bạn là \(n = 30\). Số anh, chị, em ruột là \({x_1} = 0;{x_2} = 1;{x_3} = 2;{x_4} = 3\) tương ứng với \({m_1} = 8;{m_2} = 12;{m_3} = 6,{m_4} = 4\). Do đó các tần số tương đối cho các giá trị \({x_1},{x_2},{x_3},{x_4}\) lần lượt là: \({f_1} = \frac{8}{{30}} \approx 26,7\% ;{f_2} = \frac{{12}}{{30}} = 40\% ;\) \({f_3} = \frac{6}{{30}} = 20\% ;{f_4} = \frac{4}{{30}} \approx 13,3\% .\) Ta có bảng tần số tương đối sau:
Nhận xét: Tần số tương đối của một giá trị là ước lượng cho xác suất xuất hiện giá trị đó. 2. Biểu đồ tần số tương đối
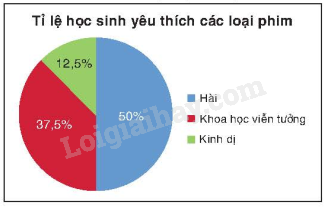
Ví dụ: Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối về loại phim yêu thích của các học sinh trong lớp 9A như sau:
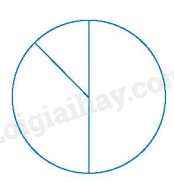
Bước 1. Xác định số đo cung tương ứng của các hình quạt biểu diễn các tần số tương đối cho mỗi loại phim: Hài: \(360^\circ .50\% = 180^\circ \); Khoa học viễn tưởng: \(360^\circ .37,5\% = 135^\circ \); Kinh dị: \(360^\circ .12,5\% = 45^\circ \). Bước 2. Vẽ hình tròn và chia hình tròn thành các hình quạt.
Bước 3. Định dạng các hình quạt tròn, ghi tỉ lệ phần trăm, chú giải và tiêu đề.
|