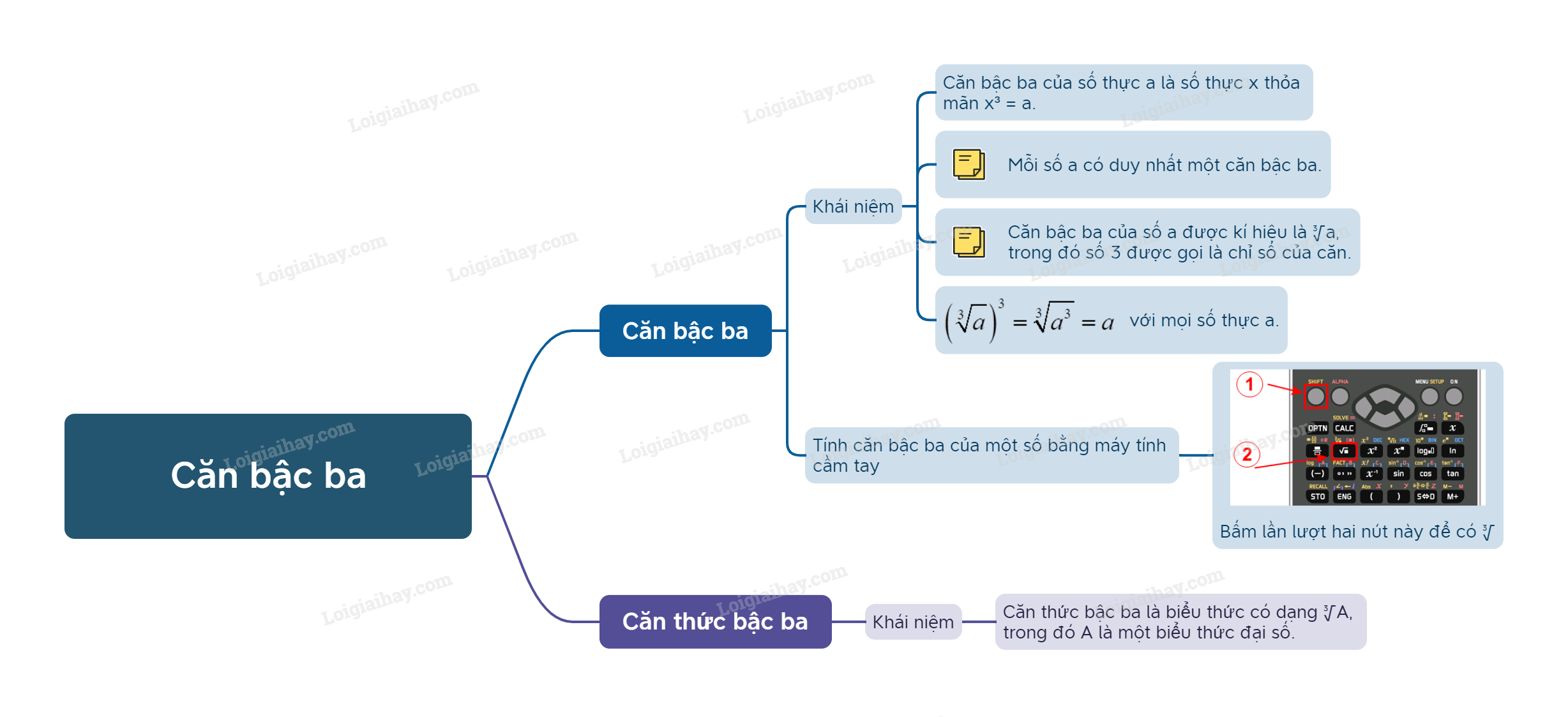
Lý thuyết Căn bậc ba Toán 9 Chân trời sáng tạo1. Căn bậc ba của một số Khái niệm căn bậc ba của một số thực GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.XYZ và nhận về những phần quà hấp dẫn 1. Căn bậc ba của một số Khái niệm căn bậc ba của một số thực
Trong kí hiệu \(\sqrt[3]{a}\), số 3 được gọi là chỉ số căn. Phép toán tìm căn bậc ba của một số gọi là phép khai căn bậc hai. Chú ý: Từ định nghĩa căn bậc ba, ta có \({\left( {\sqrt[3]{a}} \right)^3} = \sqrt[3]{{{a^3}}} = a\). Ví dụ: \(\sqrt[3]{{64}} = \sqrt[3]{{{4^3}}} = 4\); \(\sqrt[3]{{ - 27}} = \sqrt[3]{{{{\left( { - 3} \right)}^3}}} = - 3\). 2. Tính căn bậc ba của một số bằng máy tính cầm tay Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.
Ví dụ:
3. Căn thức bậc ba Khái niệm
Ví dụ: Với \(x = 60\), giá trị của \(\sqrt[3]{{2x + 5}}\) là: \(\sqrt[3]{{2.60 + 5}} = \sqrt[3]{{125}} = \sqrt[3]{{{5^3}}} = 5\).    Chia sẻ Bình luận
Tham Gia Group Dành Cho Lớp 9 - Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
