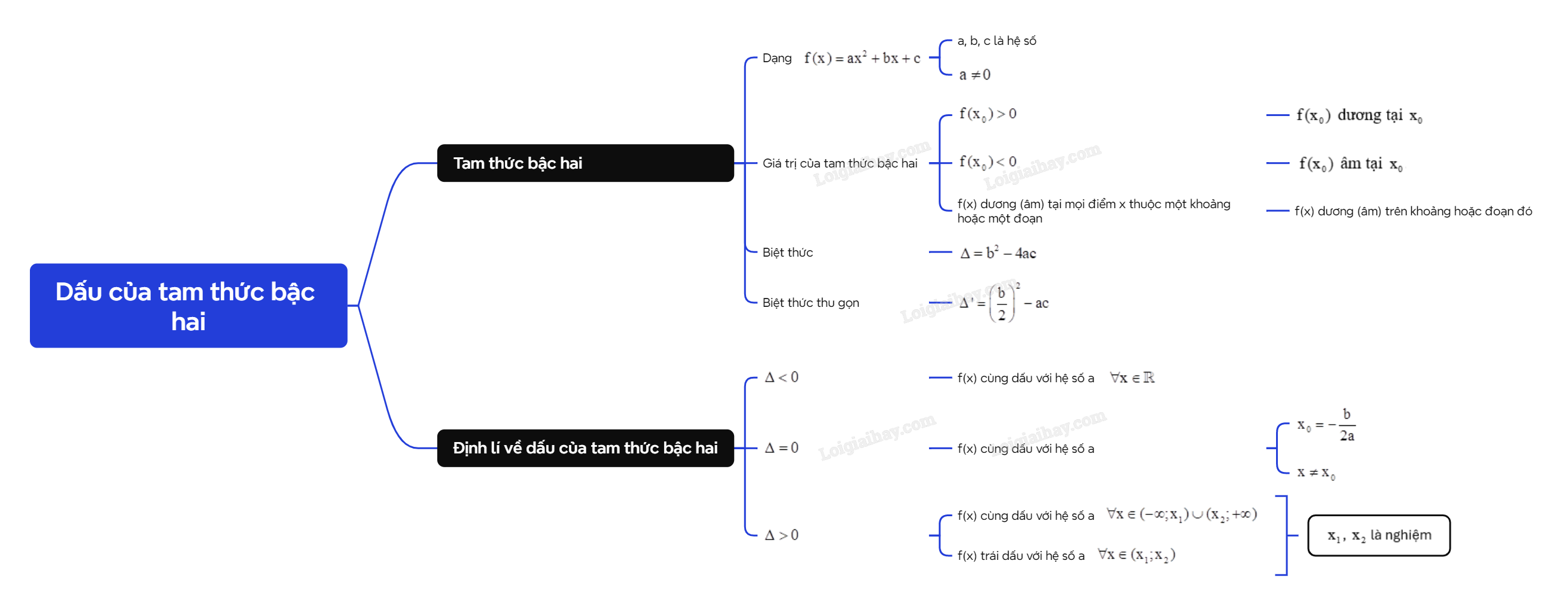
Lý thuyết Dấu của tam thức bậc hai - SGK Toán 10 Chân trời sáng tạo

A. Lý thuyết

1. Tam thức bậc hai

Khi thay x bằng giá trị \({x_0}\) vào f(x), ta được \(f({x_0}) = a{x_0}^2 + b{x_0} + c\), gọi là giá trị của tam thức bậc hai.

- Nếu \(f({x_0}) > 0\) thì ta nói \(f({x_0})\) dương tại \({x_0}\).

- Nếu \(f({x_0}) < 0\) thì ta nói \(f({x_0})\) âm tại \({x_0}\).

- Nếu f(x) dương (âm) tại mọi điểm x thuộc một khoảng hoặc một đoạn thì ta nói f(x) dương (âm) trên khoảng hoặc đoạn đó.

2. Định lí về dấu của tam thức bậc hai

Mối quan hệ giữa dấu của tam thức bậc hai  với dấu của hệ số a trong từng trường hợp của  được phát biểu trong định lí về dấu của tam thức bậc hai sau đây:

Chú ý: Để xét dấu tam thức bậc hai \(f(x) = a{x^2} + bx + c\)\((a \ne 0)\), ta thực hiện các bước sau:

B1: Tính và xét dấu của biệt thức \(\Delta \).

B2: Xác định nghiệm của f(x) (nếu có).

B3: Xác định dấu của hệ số a.

B4: Xác định dấu của f(x).

B. Bài tập

Bài 1: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại x = 2.

A. \(3x + 2\sqrt x  + 1\)

B. \( - 5{x^4} + 3{x^2} + 4\)

C. \( - \frac{2}{3}{x^2} + 7x - 4\)

D. \({\left( {\frac{1}{x}} \right)^2} + 2\frac{1}{x} + 3\)

Giải:

\( - \frac{2}{3}{x^2} + 7x - 4\) là tam thức bậc hai với \(a =  - \frac{2}{3},b = 7,c =  - 4\).

\(f(2) =  - \frac{2}{3}{.2^2} + 7.2 - 4 = \frac{{22}}{3} > 0\) nên f(x) dương tại x = 2.

Bài 2: Xét dấu các tam thức bậc hai sau đây:

a) \({x^2} + x + 1\).

b) \( - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\).

c) \(2{x^2} + 6x - 8\).

Giải:

a) \(f(x) = {x^2} + x + 1\) có \(\Delta  =  - 3 < 0\) và \(a = 1 > 0\) nên f(x) > 0 với mọi \(x \in \mathbb{R}\).

b) \(f(x) =  - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\) có \(\Delta  = 0\) và \(a =  - \frac{3}{2} < 0\) nên f(x) có nghiệm kép x = 3 và f(x) < 0 với mọi \(x \ne 3\).

c) Dễ thấy \(f(x) = 2{x^2} + 6x - 8\) có \(\Delta ' = 25 > 0\), a = 2 > 0 và có hai nghiệm phân biệt \({x_1} =  - 4\), \({x_2} = 1\). Do đó ta có bảng xét dấu:

Suy ra f(x) > 0 với mọi \(x \in ( - \infty ; - 4) \cup (1; + \infty )\) và f(x) < 0 với mọi \(x \in ( - 4;1)\).