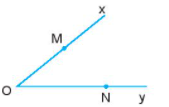
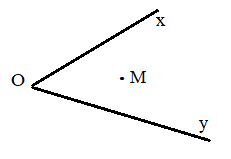
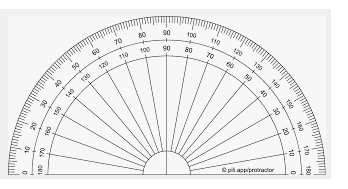
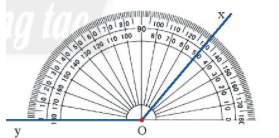
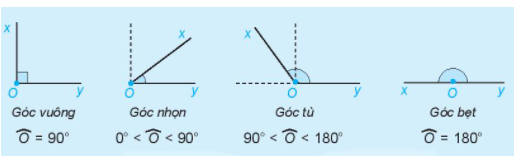
Lý thuyết Góc Toán 6 Cánh diềuLý thuyết Góc Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu I. Góc Góc là hình gồm hai tia chung gốc. Gốc chung của hai tia gọi là đỉnh của góc. Hai tia là hai cạnh của góc. Chú ý: Trong hình trên: - Góc \(xOy\) (hoặc \(yOx\)) được kí hiệu là \(\widehat {xOy}\) (hoặc \(\angle xOy\)). - Hai tia \(Ox\) và \(Oy\) được gọi là hai cạnh của góc. Gốc chung của hai tia được gọi là đỉnh của góc. - Góc \(xOy\) còn có cách gọi khác là: góc \(AOB\), góc \(O\), góc \(yOx\), góc \(BOA\). II. Cách vẽ gócĐể vẽ \(\widehat {xOy}\), ta vẽ điểm \(O\) trên giấy hoặc bảng, từ điểm \(O\) vẽ hai tia \(Ox\) và \(Oy\). Ta được \(\widehat {xOy}\). III. Góc bẹtKhi \(Ox\) và \(Oy\) là hai tia đối nhau, ta có góc bẹt \(xOy\). IV. Điểm trong của gócCho góc xOy khác góc bẹt. Điểm M được gọi là điểm trong của góc xOy không bẹt nếu tia OM cắt một đoạn thẳng nối hai điểm trên hai cạnh tại một điểm nằm giữa hai điểm đó. Ví dụ: Trong hình dưới đây, M là điểm trong của \(\widehat {xOy}\). V. Thước đo góc. Cách đo góc. Số đo góca) Thước đo góc Thước đo góc có dạng nửa hình tròn và được chia đều thành 180 phần bằng nhau, mỗi phần ứng với \({1^o}\). b) Cách đo góc - Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc. - Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc như trên. - Bước 3: Xác định xem cạnh còn lại của góc (cạnh Ox) đi qua vạch chỉ số nào trên thước đo góc, ta sẽ được số đo của góc đó. Ví dụ: Trong hình bên trên, tia Ox đi qua vạch chỉ số 130, vậy góc xOy có số đo là 130°. Ta viết \(\widehat {xOy} = {130^o}.\) c) Số đo góc Mỗi góc có một số đo. Số đo của góc bẹt là \({180^o}\). Số đo của mỗi góc không vượt quá \({180^o}\). VI. Các góc đặc biệt- Góc có số đo bằng \({90^o}\) là góc vuông - Góc bẹt có số đo bằng \({180^o}\) - Góc có số đo nhỏ hơn \({90^o}\) là góc nhọn - Góc có số đo lơn hơn \({90^o}\) nhưng nhỏ hơn \({180^o}\) là góc tù.
|