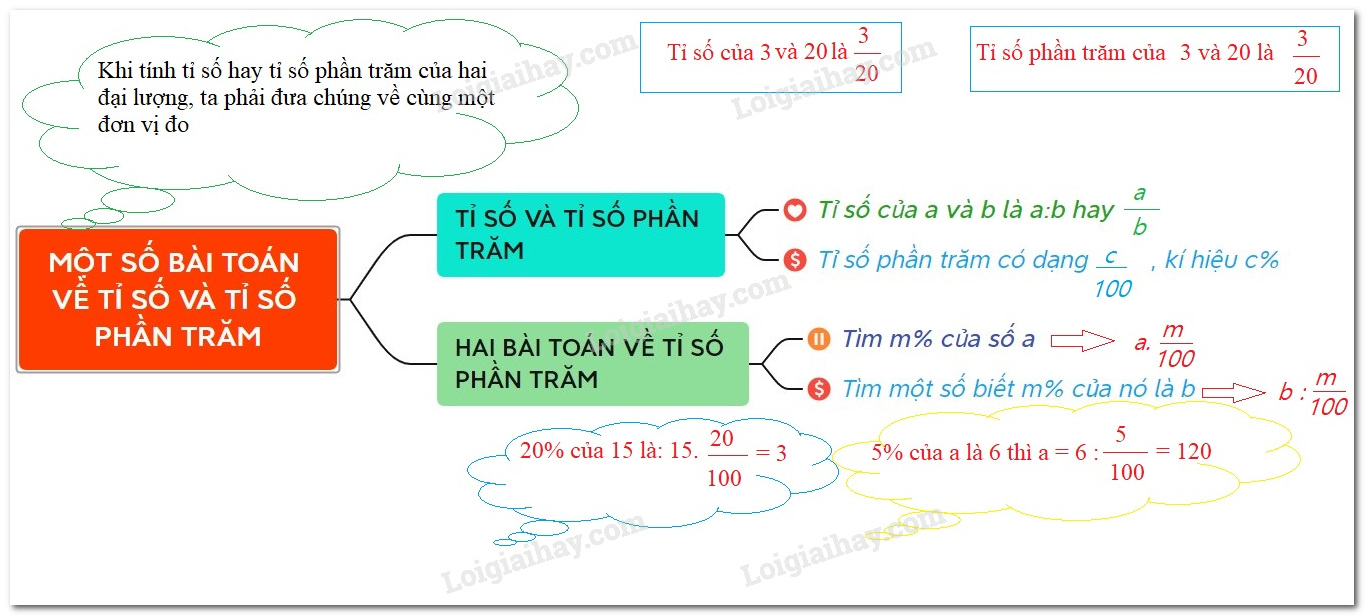
Lý thuyết Hai bài toán về phân số Toán 6 Cánh diềuLý thuyết Hai bài toán về phân số Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu Tổng hợp đề thi học kì 2 lớp 6 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... I. Tính giá trị phân số của một số cho trướcMuốn tìm mn của số b cho trước, ta tính b.mn (m,n∈N,n≠0) Ví dụ: a) 23 của 8,7 là: 8,7.23=(8,7:3).2=2,9.2=5,8. b) 23 của −152 là: 23.−152=−5. II. Tìm một số khi biết giá trị phân số của nóMuốn tìm một số khi biết giá trị mn của nó bằng a, ta tính a:mn (m,n∈N∗). Ví dụ: Tìm một số biết 23 của nó bằng 7,2 Số cần tìm là: 7,2:23=7,2.32=10,8. III. Tìm giá trị phần trăm của một sốMuốn tìm giá trị a% của số b, ta tính: b.a%=b.a100 Ví dụ: 99,99% của 3,75 là: 3,75.99,99100=3,749625 IV. Tìm một số khi biết giá trị phần trăm của số đóMuốn tìm mốt số khi biết m% của số đó là b, ta tính: b:m100 Ví dụ: Số có giá trị 2,5% bằng 200 là số: 200:2,5100=8000 V. Sử dụng tỉ số phần trăm trong thực tếTỉ số phần trăm thường được sử dụng trong đời sống để giải quyết một số bài toán như: - Lãi suất tín dụng - Thành phần các chất hóa học.    Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 6 chương trình mới trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 6 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|
