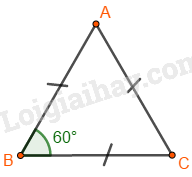
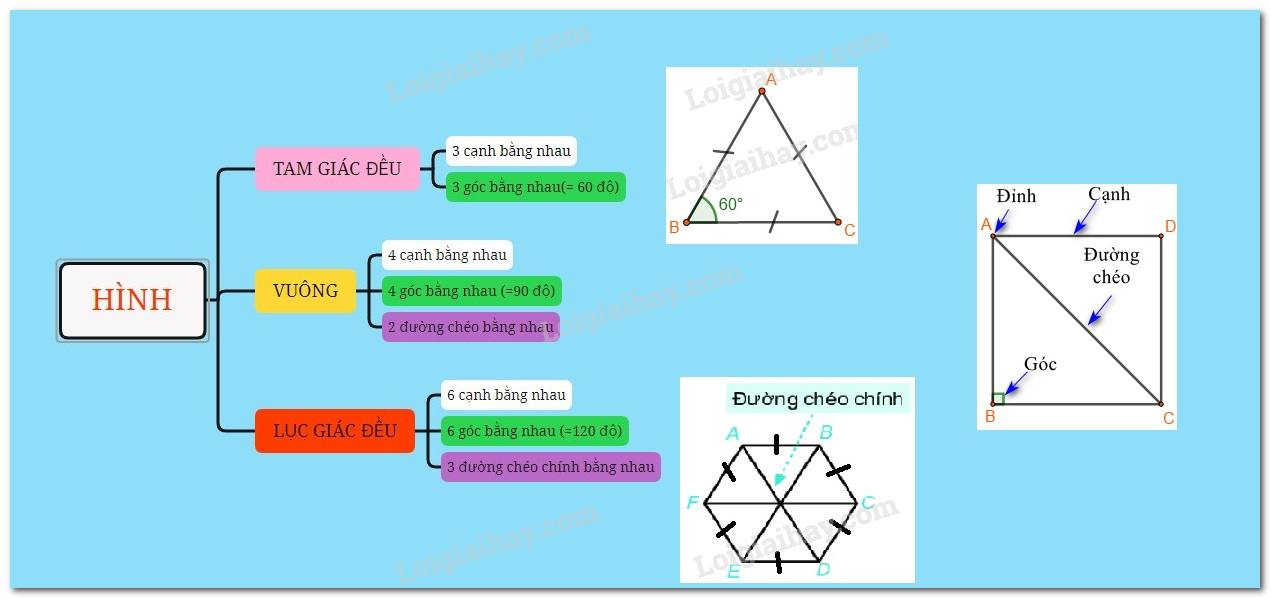
Lý thuyết Hình tam giác đều. Hình vuông, Hình lục giác đều Toán 6 KNTT với cuộc sống

 1. Hình tam giác đều

Các yếu tố cơ bản của tam giác đều:

- Ba cạnh bằng nhau.

- Ba góc bằng nhau và bằng ${60^0}$

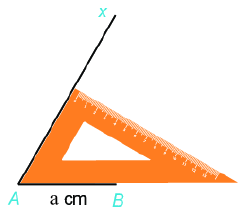
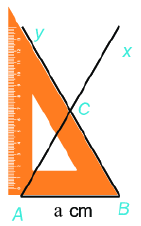
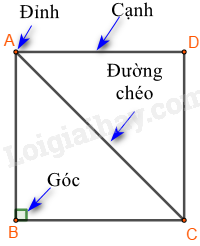
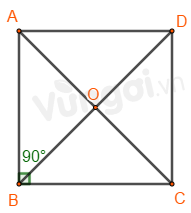
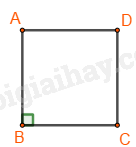
Cách vẽ tam giác đều $ABC$ khi biết độ dài một cạnh bằng $a$.

Bước 1: Vẽ đoạn thẳng $AB = a$.

Bước 2: Dùng ê ke có góc ${60^0}$, vẽ góc $BAx$ bằng ${60^0}$.

Bước 3: Vẽ góc $ABy = {60^0}$ hai tia $Ax,By$ cắt nhau tại $C$, ta được tam giác đều $ABC$.

2. Hình vuông

Một số yếu tố cơ bản của hình vuông

- Bốn cạnh bằng nhau.

- Bốn góc bằng nhau và bằng ${90^0}$.

- Hai đường chéo bằng nhau.

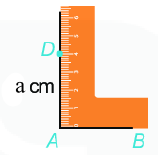
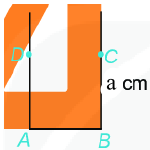
Cách vẽ hình vuông khi biết độ dài cạnh bằng $a$:

Bước 1: Vẽ đoạn thẳng $AB = a\left( {cm} \right)$

Bước 2: Vẽ đường thẳng vuông góc với $AB$ tại $A$. Xác định điểm $D$ trên đường thẳng đó sao cho $AD = a\left( {cm} \right)$.

Bước 3: Vẽ đường thẳng vuông góc với $AB$ tại $B$. Xác định điểm $C$ trên đường thẳng đó sao cho $BC = a\left( {cm} \right)$.

Bước 4: Nối $C$ với $D$ ta được hình vuông $ABCD$.

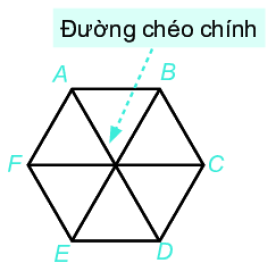
3. Hình lục giác đều

Một số yếu tố cơ bản của hình lục giác đều:

- Sáu cạnh bằng nhau.

- Sáu góc bằng nhau và bằng ${120^0}$.

- Ba đường chéo chính bằng nhau.

- AC, BD, CE, DF, EA,FB là các đường chéo phụ của ABCDEF.