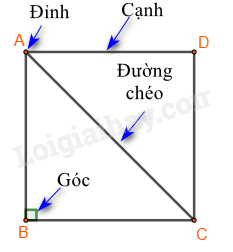
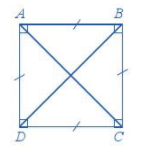
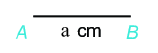
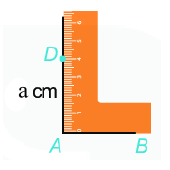
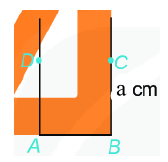
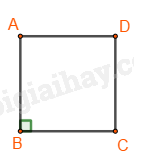
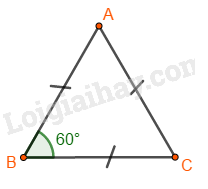
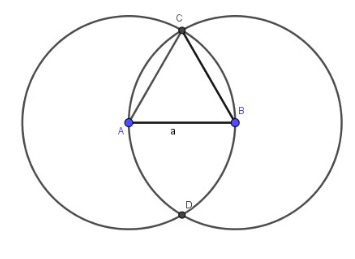
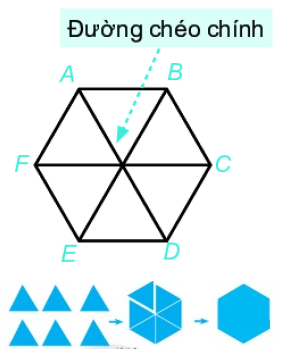
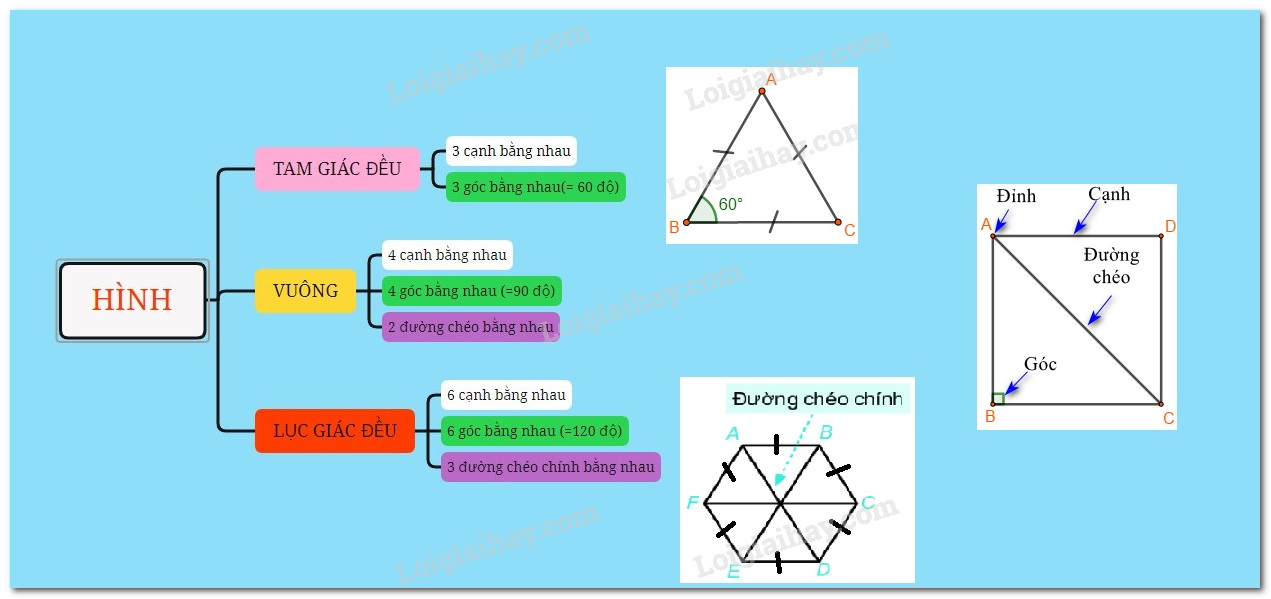
Lý thuyết Hình vuông- Tam giác đều- Lục giác đều Toán 6 Chân trời sáng tạoLý thuyết Hình vuông- Tam giác đều- Lục giác đều Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu I. Hình vuông 1.Nhận biết hình vuông Bốn cạnh bằng nhau: \(AB = BC = CD = DA;\) Hai cạnh đối \(AB\) và \(CD;\) \(AD\) và \(BC\) song song với nhau; Hai đường chéo bằng nhau: \(AC = BD;\) Bốn góc ở các đỉnh \(A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\) là góc vuông. 2. Vẽ hình vuông Vẽ bằng ê ke hình vuông \(ABCD\), biết độ dài cạnh bằng \(a{\rm{ }}cm\). Bước 1: Vẽ đoạn thẳng \(AB = a\left( {cm} \right)\) Bước 2: Vẽ đường thẳng vuông góc với \(AB\) tại \(A\). Xác định điểm \(D\) trên đường thẳng đó sao cho \(AD = a\left( {cm} \right)\). Bước 3: Vẽ đường thẳng vuông góc với \(AB\) tại \(B\). Xác định điểm \(C\) trên đường thẳng đó sao cho \(BC = a\left( {cm} \right)\). Bước 4: Nối \(C\) với \(D\) ta được hình vuông \(ABCD\). II. Tam giác đều1. Nhận biết tam giác đều Trong tam giác đều: + Ba cạnh bằng nhau + Ba góc bằng nhau. Ví dụ: Tam giác đều \(ABC\) có: + Ba cạnh bằng nhau: \(AB = BC = CA\). + Ba góc ở các đỉnh \(A,B,\,C\) bằng nhau. 2. Vẽ tam giác đều Cách vẽ tam giác đều cạnh \(a\,(cm)\) bằng thước và compa: Bước 1. Dùng thước vẽ đoạn thẳng AB = a cm Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ. Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC. III. Lục giác đềuLục giác đều \(ABCDEF\) có: - Sáu đỉnh A, B, C, D, E, F - Sáu cạnh bằng nhau: \(AB = BC = CD = DE = EF\). - Sáu góc ở các đỉnh A, B, C, D, E, F bằng nhau. - Ba đường chéo chính bằng nhau \(AD = BE = CF\).
|