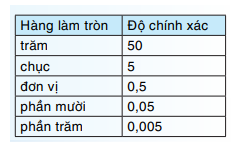
Lý thuyết Làm quen với số thập phân vô hạn tuần hoàn SGK Toán 7 - Kết nối tri thức1. Số thập phân vô hạn tuần hoàn 1. Số thập phân vô hạn tuần hoàn Ví dụ: Các số thập phân đã học như -4,3 ; 0,35;… còn được gọi là số thập phân hữu hạn. Các số -0,2(7) ; 1,3(18) ; 5,(1) ;…. là những số thập phân vô hạn tuần hoàn với chu kì lần lượt là 7 ; 18 ; 1. + Mỗi số thập phân vô hạn tuần hoàn biểu diễn 1 số hữu tỉ Chú ý: + Mọi số hữu tỉ đều viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn. + Nếu phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố nào khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân hữu hạn. Ví dụ: \(\frac{3}{{80}} = \frac{3}{{{2^4}.5}} = \frac{{{{3.5}^3}}}{{{2^4}{{.5.5}^3}}} = \frac{{375}}{{10000}} = 0,0375\) + Nếu phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn. Ví dụ: \(\frac{7}{{30}} = 0,2333.... = 0,2(3)\) 2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước Khi làm tròn đến môt hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn. Ví dụ: Làm tròn số 2,13452….với độ chính xác 0,005, tức là làm tròn số 2,13452…. đến hàng phân trăm, ta được 2,13.
|