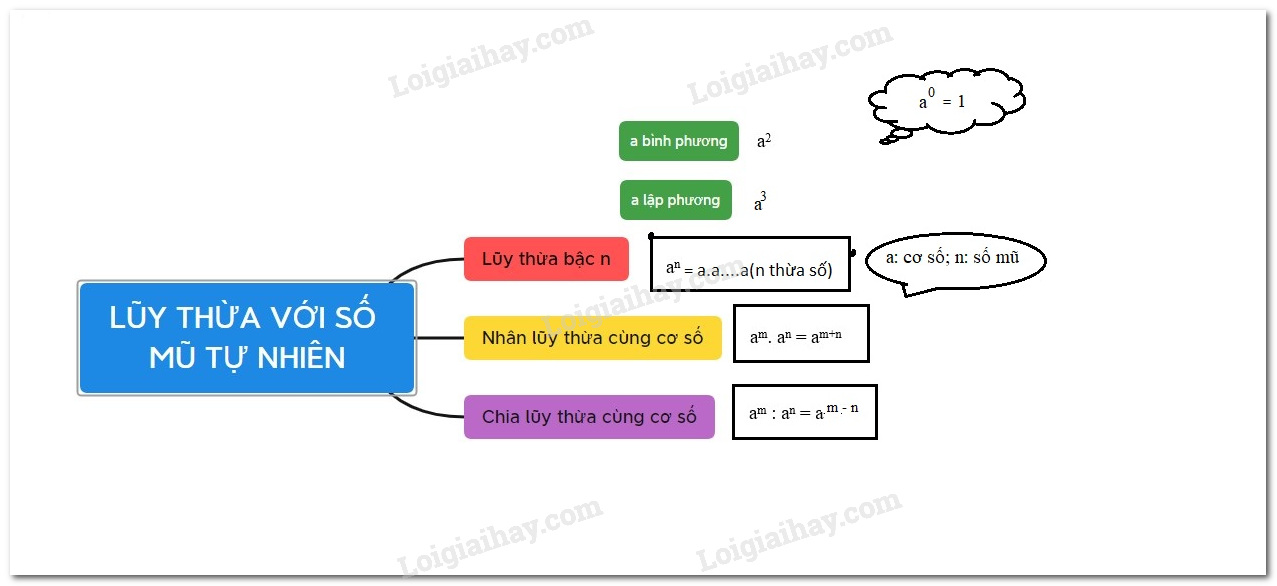
Lý thuyết Lũy thừa với số mũ tự nhiên Toán 6 KNTT với cuộc sốngLý thuyết Lũy thừa với số mũ tự nhiên Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu 1. Lũy thừa với số mũ tự nhiên Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a: \({a^n} = a.a \ldots ..a\) (\(n\) thừa số \(a\) ) (\(n \ne 0\)) \({a^n}\) đọc là “a mũ n” hoặc “a lũy thừa n”. \(a\) được gọi là cơ số. \(n\) được gọi là số mũ. Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa. \({a^1} = a\) \({a^2} = a.a\) gọi là “\(a\) bình phương” (hay bình phương của \(a\)). \({a^3} = a.a.a\) gọi là “\(a\) lập phương” (hay lập phương của \(a\)). Quy ước: \({a^1} = a\); \({a^0} = 1\left({a \ne 0} \right).\) Ví dụ: Tính \({2^3}\). Số trên là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có: \({2^3} = 2.2.2 = 8\) 2. Nhân hai lũy thừa cùng cơ số \({a^m}.{a^n} = {a^{m + n}}\) Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ. Ví dụ: \({3.3^5} = {3^1}{.3^5} = {3^{1 + 5}} = {3^6}.\) 3. Chia hai lũy thừa cùng cơ số \({a^m}:{a^n} = {a^{m - n}}\) \(\left( {a \ne 0;\,m \ge n \ge 0} \right)\) Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau. Ví dụ: \({3^5}:3 = {3^5}:{3^1} = {3^{5 - 1}} = {3^4} = 3.3.3.3 = 81\)
|