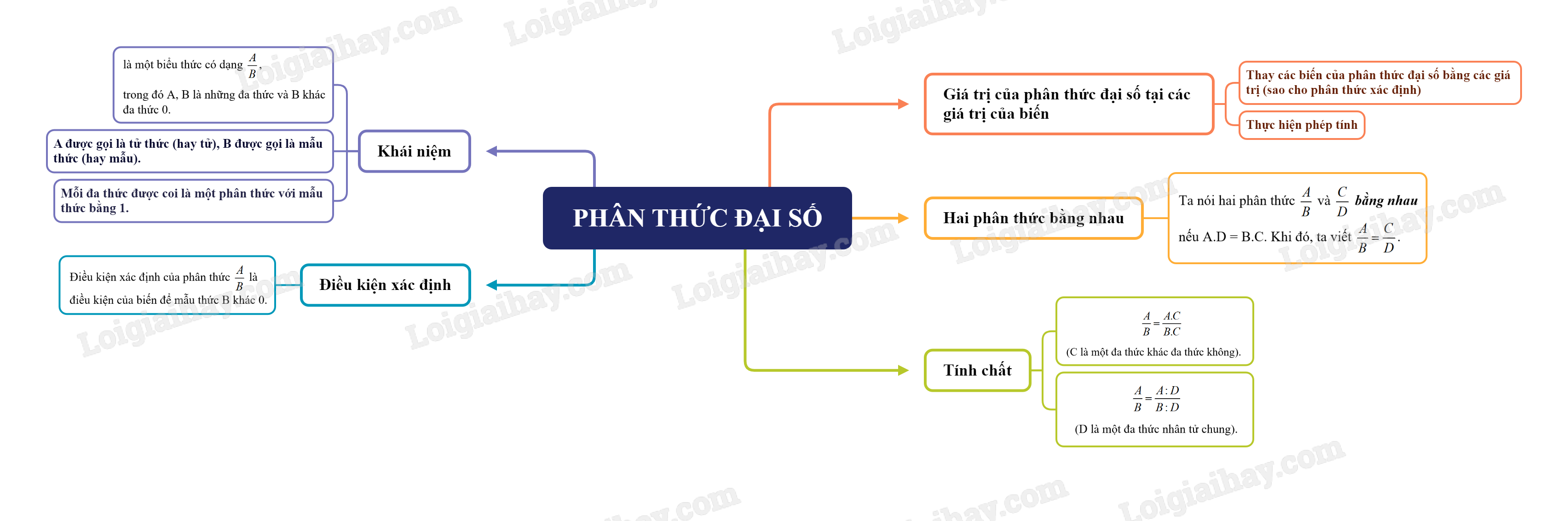
Lý thuyết Phân thức đại số SGK Toán 8 - Chân trời sáng tạoPhân thức đại số là gì? 1. Khái niệm phân thức đại số Một phân thức đại số (hay còn gọi là phân thức) là một biểu thức có dạng \(\frac{A}{B}\), trong đó A, B là những đa thức và B khác đa thức 0. A được gọi là tử thức (hay tử), B được gọi là mẫu thức (hay mẫu). Chú ý: Mỗi đa thức được coi là một phân thức với mẫu thức bằng 1. Ví dụ: \(\frac{{2x + 1}}{{x - 3}};\frac{{ab}}{{a + b}};{x^2} + 3x + 2;\sqrt 2 \) là các phân thức đại số. \(\sqrt x ;\sqrt[3]{x}\) không phải là phân thức vì \(\sqrt x ;\sqrt[3]{x}\) không phải là đa thức. 2. Điều kiện xác định của phân thức Điều kiện xác định của phân thức \(\frac{A}{B}\) là điều kiện của biến để mẫu thức B khác 0. Khi thay các biến của phân thức đại số bằng các giá trị nào đó (sao cho phân thức xác định), rồi thực hiện các phép tính thì ta nhận được giá trị của phân thức đại số đó tại các giá trị của biến. Ví dụ: Phân thức P = \(\frac{{x + 3}}{{x - 1}}\) xác định khi \(x - 1 \ne 0\) hay \(x \ne 1\) Tại x = 3, \(P = \frac{{3 + 3}}{{3 - 1}} = \frac{6}{2} = 3\) 3. Hai phân thức bằng nhau Ta nói hai phân thức \(\frac{A}{B}\) và \(\frac{C}{D}\) bằng nhau nếu A.D = B.C. Khi đó, ta viết \(\frac{A}{B} = \frac{C}{D}\). Ví dụ: Hai phân thức \(\frac{{x{y^2}}}{{xy + y}}\) và \(\frac{{xy}}{{x + 1}}\) bằng nhau. 4. Tính chất Khi nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho. \(\frac{A}{B} = \frac{{A.C}}{{B.C}}\) (C là một đa thức khác đa thức không). Khi chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho. \(\frac{A}{B} = \frac{{A:D}}{{B:D}}\) (D là một đa thức nhân tử chung). Ví dụ: Để biến đổi phân thức \(\frac{{x - y}}{{{y^2} - {x^2}}}\) thành \(\frac{{ - 1}}{{x + y}}\), ta chia cả tử và mẫu của phân thức \(\frac{{x - y}}{{{y^2} - {x^2}}}\) cho y – x, khi đó \(\frac{{x - y}}{{{y^2} - {x^2}}} = \frac{{ - (y - x)}}{{(y - x)(y + x)}} = \frac{{ - 1}}{{x + y}}\)
|