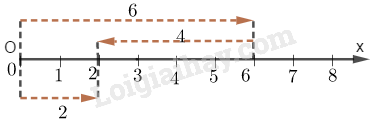
Lý thuyết Phép cộng và phép trừ số tự nhiên Toán 6 KNTT với cuộc sống

 1. Phép cộng

$a + b = c$

(số hạng) + (số hạng) = (tổng)

Minh họa trên tia số:

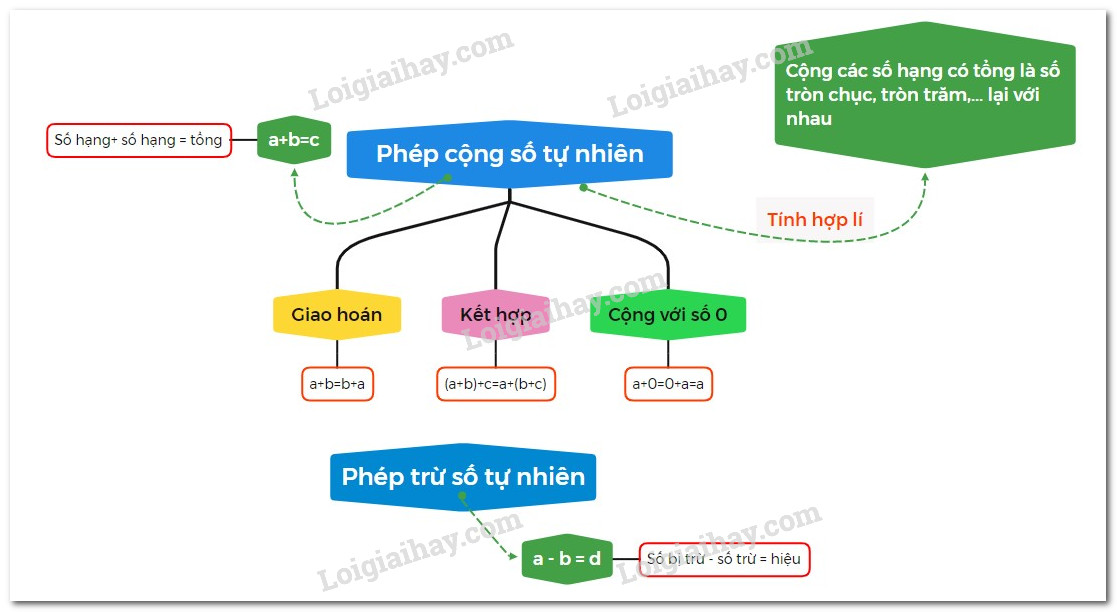
Tính chất của phép cộng:

Giao hoán: $a + b = b + a$

Kết hợp: $\left( {a + b} \right) + c = a + \left( {b + c} \right) = a + b + c$

 $a + b + c$ được gọi là tổng của ba số $a,b,c$

Cộng với số 0: $a + 0 = 0 + a = a$

Lưu ý: Khi cộng nhiều số, ta nên nhóm các số hạng có tổng là số chẵn tròn chục, tròn trăm,...(nếu có).

Ví dụ:

Tính một cách hợp lí: 12+25+15+28

Nhận xét: Ta thấy nếu tính riêng 12+28 và 25+15 thì được: 12+28=40 và 25+15=40 kết quả của hai phép tính này là tròn chục nên ta thực hiện phép tính sau:

12+25+15+28

= 12+28+25+15 (Đổi vị trí của các số 25, 15, 28: Tính chất giao hoán)

= (12+28)+(25+15) (Kết hợp)

= 40+40

= 80

2. Phép trừ

Cho hai số tự nhiên $a$ và $b,$  nếu có số tự nhiên $x$ sao cho $b + x = a$ thì ta có phép trừ

$a - b = x$

(số bị trừ) - (số trừ) = (hiệu)

Chú ý: Điều kiện để thực hiện được phép trừ là số bị trừ lớn hơn hoặc bằng số trừ.

Minh họa trên tia số: