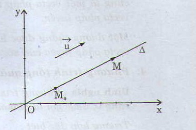
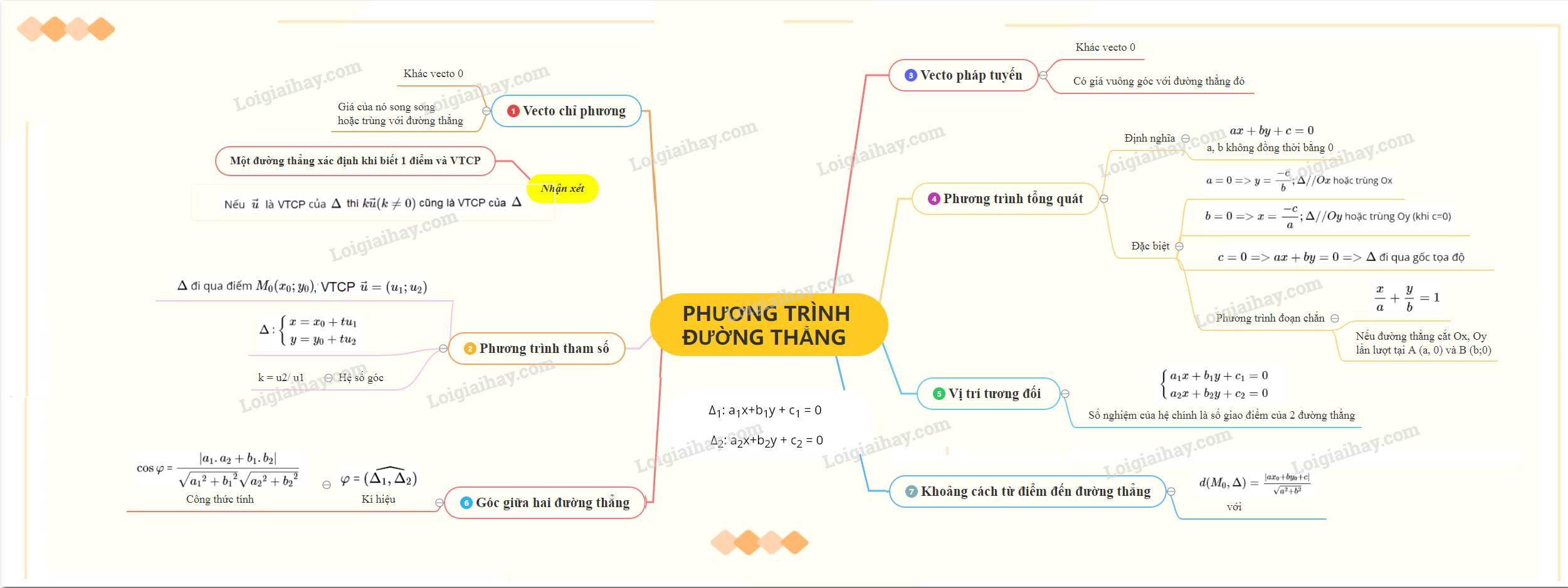
Lý thuyết phương trình đường thẳngVectơ chỉ phương của đường thẳng A. Lý thuyết1. Vectơ chỉ phương của đường thẳngĐịnh nghĩa: Vectơ \(\vec{u}\) được gọi là vectơ chỉ phương của đường thẳng \(∆\) nếu \(\vec{u}\) ≠ \(\vec{0}\) và giá của \(\vec{u}\) song song hoặc trùng với \(∆\).
Nhận xét : - Nếu \(\vec{u}\) là một vectơ chỉ phương của đường thẳng \(∆\) thì \(k\vec{u} ( k≠ 0)\) cũng là một vectơ chỉ phương của \(∆\), do đó một đường thẳng có vô số vectơ chỉ phương. - Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ chỉ phương của đường thẳng đó. 2. Phương trình tham số của đường thẳng- Phương trình tham số của đường thẳng \(∆\) đi qua điểm \(M_0(x_0 ;y_0)\) và nhận vectơ \(\vec{u} = (u_1; u_2)\) làm vectơ chỉ phương là: \(∆\): \(\left\{\begin{matrix} x= x_{0}+tu_{1}& \\ y= y_{0}+tu_{2}& \end{matrix}\right.\) - Khi \(u_1≠ 0\) thì tỉ số \(k= \dfrac{u_{2}}{u_{1}}\) được gọi là hệ số góc của đường thẳng. Từ đây, ta có phương trình đường thẳng \(∆\) đi qua điểm \(M_0(x_0 ;y_0)\) và có hệ số góc k là: \(y – y_0 = k(x – x_0)\). Chú ý: Ta đã biết hệ số góc \(k = \tan α\) với góc \(α\) là góc của đường thẳng \(∆\) hợp với chiều dương của trục \(Ox\). 3. Vectơ pháp tuyến của đường thẳngĐịnh nghĩa: Vectơ \(\vec{n}\) được gọi là vectơ pháp tuyến của đường thẳng \(∆\) nếu \(\vec{n}\) ≠ \(\vec{0}\) và \(\vec{n}\) vuông góc với vectơ chỉ phương của \(∆\). Nhận xét: - Nếu \(\vec{n}\) là một vectơ pháp tuyến của đường thẳng \(∆\) thì k\(\vec{n}\) \((k ≠ 0)\) cũng là một vectơ pháp tuyến của \(∆\), do đó một đường thẳng có vô số vec tơ pháp tuyến. - Một đường thẳng được hoàn toàn xác định nếu biết một và một vectơ pháp tuyến của nó. 4. Phương trình tổng quát của đường thẳngĐịnh nghĩa: Phương trình \(ax + by + c = 0\) với \(a\) và \(b\) không đồng thời bằng \(0\), được gọi là phương trình tổng quát của đường thẳng. Trường hợp đặc biết: + Nếu \(a = 0 => y = \dfrac{-c}{b}; ∆ // Ox\) hoặc trùng Ox (khi c = 0). + Nếu \(b = 0 => x = \dfrac{-c}{a}; ∆ // Oy\) hoặc trùng Oy (khi c = 0). + Nếu \(c = 0 => ax + by = 0 => ∆\) đi qua gốc tọa độ. + Nếu \(∆\) cắt \(Ox\) tại \(A(a; 0)\) và \(Oy\) tại \(B (0; b)\) thì ta có phương trình đoạn chắn của đường thẳng \(∆\): \(\dfrac{x}{a} + \dfrac{y}{b} = 1\). 5. Vị trí tương đối của hai đường thẳngXét hai đường thẳng ∆1 và ∆2 có phương trình tổng quát lần lượt là: a1x + b1y + c1 = 0 và a2x + b2y + c2 = 0. Điểm \(M_0(x_0 ;y_0)\) là điểm chung của ∆1 và ∆2 khi và chỉ khi \((x_0 ;y_0)\) là nghiệm của hệ hai phương trình: (1) \(\left\{\begin{matrix} a_{1}x+b_{1}y +c_{1} = 0& \\ a_{2}x+b_{2}y+c_{2}= 0& \end{matrix}\right.\) Ta có các trường hợp sau: a) Hệ (1) có một nghiệm: ∆1 cắt ∆2. b) Hệ (1) vô nghiệm: ∆1 // ∆2. c) Hệ (1) có vô số nghiệm: ∆1 \( \equiv \) ∆2. 6. Góc giữa hai đường thẳngHai đường thẳng ∆1 và ∆2 cắt nhau tạo thành 4 góc. Nếu ∆1 không vuông góc với ∆2 thì góc nhọn trong số bốn góc đó được gọi là góc giữa hai đường thẳng ∆1 và ∆2. Nếu ∆1 vuông góc với ∆2 thì ta nói góc giữa ∆1 và ∆2 bằng 900. Trường hợp ∆1 và ∆2 song song hoặc trùng nhau thì ta quy ước góc giữa ∆1 và ∆2 bằng 00. Như vậy góc giữa hai đường thẳng luôn bé hơn hoặc bằng 900. Góc giữa hai đường thẳng ∆1 và ∆2 được kí hiệu là \(\widehat{(\Delta _{1},\Delta _{2})}\). Cho hai đường thẳng: ∆1: a1x + b1y + c1 = 0 và ∆2: a2x + b2y + c2 = 0. Đặt \(\varphi\) = \(\widehat{(\Delta _{1},\Delta _{2})}\). \(\cos \varphi\) = \(\dfrac{|a_{1}.a_{2}+b_{1}.b_{2}|}{\sqrt{{a_{1}}^{2}+{b_{1}}^{2}}\sqrt{{a_{2}}^{2}+{b_{2}}^{2}}}\). Chú ý: + \({\Delta _1} \bot {\Delta _2} \Leftrightarrow {n_1} \bot {n_2}\) \( \Leftrightarrow {a_1}.{a_2} + {b_1}.{b_2} = 0\). + Nếu \({\Delta _1}\) và \({\Delta _2}\) có phương trình y = k1 x + m1 và y = k2 x + m2 thì \({\Delta _1} \bot {\Delta _2} \Leftrightarrow {k_1}.{k_2} = - 1\). 7. Công thức tính khoảng cách từ một điểm đến một đường thẳngTrong mặt phẳng \(Oxy\) cho đường thẳng \(∆\) có phương trình \(ax+by+c=0\) và điểm \(M_0(x_0 ;y_0)\). Khoảng cách từ điểm \(M_0\) đến đường thẳng \(∆\) kí hiệu là \(d(M_0,∆)\), được tính bởi công thức: \(d(M_0,∆)=\frac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}\). B. Bài tập vận dụngBài 1: a) Cho đường thẳng \(\Delta \) có vecto pháp tuyến \(\overrightarrow n = \left( {\frac{1}{2}; - \frac{5}{2}} \right)\). Tìm vecto chỉ phương của \(\Delta \). b) Cho đường thẳng d có vecto chỉ phương \(\overrightarrow u = (1;3)\). Tìm hai vecto pháp tuyến của d. Giải: a) \(\Delta \) có vecto pháp tuyến \(\overrightarrow n = \left( {\frac{1}{2}; - \frac{5}{2}} \right)\), suy ra \(\Delta \) cũng có vecto pháp tuyến \(2\overrightarrow n = \left( {1; - 5} \right)\) và có vecto chỉ phương \(\overrightarrow u = (5;1)\). b) Hai vecto pháp tuyến của d là \(\overrightarrow n = (3; - 1)\), \( - \overrightarrow n = ( - 3;1)\). Bài 2: Lập phương trình đường thẳng \(\Delta \) thỏa mãn: a) Đi qua M(-2;-3) và có \(\overrightarrow n = (2;5)\) là vecto pháp tuyến. b) Đi qua M(3;-5) và có \(\overrightarrow u = (2; - 4)\) là vecto chỉ phương. c) Đi qua A(-3;4) và B(1;-1). Giải: a) Phương trình \(\Delta \) là \(2(x + 2) + 5(y + 3) = 0 \Leftrightarrow 2x + 5y + 19 = 0\). b) Phương trình \(\Delta \) là \(\frac{{x - 3}}{2} = \frac{{y + 5}}{{ - 4}} \Leftrightarrow 4x + 2y - 2 = 0 \Leftrightarrow 2x + y - 1 = 0\). c) Phương trình \(\Delta \) là \(\frac{{x + 3}}{{1 - ( - 3)}} = \frac{{y - 4}}{{ - 1 - 4}} \Leftrightarrow \frac{{x + 3}}{4} = \frac{{y - 4}}{{ - 5}} \Leftrightarrow 5x + 4y - 1 = 0\). Bài 3: Viết phương trình tổng quát của các đường thẳng là đồ thị hàm số bậc nhất sau: a) \({d_1}:y = 2x + 3\) b) \({d_2}:y = - \frac{1}{2}x + 5\) c) \({d_3}:y = x\) Giải: a) Ta có \(y = 2x + 3 \Leftrightarrow 2x - y + 3 = 0\). Vậy phương trình tổng quát của \({d_1}\) là \(2x - y + 3 = 0\). b) Ta có \(y = - \frac{1}{2}x + 5 \Leftrightarrow x + 2y - 10 = 0\). Vậy phương trình tổng quát của \({d_2}\) là \(x + 2y - 10 = 0\). c) Ta có \(y = x \Leftrightarrow x - y = 0\). Vậy phương trình tổng quát của \({d_3}\) là \(x - y = 0\). Bài 4: Xét vị trí tương đối của mỗi cặp đường thẳng sau: a) \({\Delta _1}:2x - y + 1 = 0\) và \({\Delta _2}: - x + 2y + 2 = 0\). b) \({\Delta _3}:x - y - 1 = 0\) và \({\Delta _4}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + 2t\end{array} \right.\). Giải: a) Đường thẳng \({\Delta _1}\) có vecto chỉ phương \(\overrightarrow {{u_1}} = (1;2)\), đường thẳng \({\Delta _2}\) có vecto chỉ phương \(\overrightarrow {{u_2}} = ( - 2; - 1)\). Do \(\frac{1}{{ - 2}} \ne \frac{2}{{ - 1}}\) nên \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương, suy ra \({\Delta _1}\) cắt \({\Delta _2}\). b) Đường thẳng \({\Delta _3}\), \({\Delta _4}\) lần lượt có vecto chỉ phương là \(\overrightarrow {{u_3}} = (1;1)\) và \(\overrightarrow {{u_4}} = (2;2)\). Suy ra \(\overrightarrow {{u_4}} = 2\overrightarrow {{u_3}} \). Chọn t = 0, ta có điểm \(M(1;3) \in {\Delta _4}\). Do \(1 - 3 - 1 \ne 0\) nên \(M(1;3) \notin {\Delta _3}\). Vậy \({\Delta _3}\) // \({\Delta _4}\). Bài 5: Xét vị trí tương đối của hai đường thẳng \({\Delta _1}:x - 2y + 1 = 0\) và \({\Delta _2}:2x - 4y + 2 = 0\). Giải: Tọa độ giao điểm của đường thẳng \({\Delta _1}\) và \({\Delta _2}\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}x - 2y + 1 = 0\\2x - 4y + 2 = 0\end{array} \right.\). Hệ trên có vô số nghiệm. Như vậy, \({\Delta _1}\) và \({\Delta _2}\) có vô số điểm chung, tức hai đường thẳng trên trùng nhau. Bài 6: Tính số đo góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trong mỗi trường hợp sau: a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 1 + \sqrt 3 {t_1}\\y = 1 + {t_1}\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 1 + \sqrt 3 {t_2}\\y = 4 - {t_2}\end{array} \right.\). b) \({\Delta _1}:3x + y - 10 = 0\) và \({\Delta _2}: - 2x + y - 7 = 0\). Giải: a) \({\Delta _1}\) có vecto chỉ phương \(\overrightarrow {{u_1}} = \left( {\sqrt 3 ;1} \right)\). \({\Delta _2}\) có vecto chỉ phương \(\overrightarrow {{u_2}} = \left( {\sqrt 3 ; - 1} \right)\). Do đó, ta có: \(\cos ({\Delta _1},{\Delta _2}) = \frac{{\left| {\sqrt 3 .\sqrt 3 + 1.( - 1)} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {1^2}} .\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{( - 1)}^2}} }} = \frac{1}{2}\). Vậy \(({\Delta _1},{\Delta _2}) = {60^o}\). b) \({\Delta _1}\) có vecto pháp tuyến \(\overrightarrow {{n_1}} = \left( {3;1} \right)\). \({\Delta _2}\) có vecto pháp tuyến \(\overrightarrow {{n_2}} = \left( { - 2;1} \right)\). Do đó, ta có: \(\cos ({\Delta _1},{\Delta _2}) = \left| {\cos (\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} )} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {3.( - 2) + 1.1} \right|}}{{\sqrt {{3^2} + {1^2}} .\sqrt {{{( - 2)}^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}\). Vậy \(({\Delta _1},{\Delta _2}) = {45^o}\). Bài 7: Tính khoảng cách từ điểm M đến đường thẳng \(\Delta \) trong mỗi trường hợp sau: a) M(-2;1) và \(\Delta :2x - 3y + 5 = 0\). b) M(1;-3) và \(\Delta :\left\{ \begin{array}{l}x = - 2 + 3t\\y = 2 - 4t\end{array} \right.\). Giải: a) Ta có: \(d(M,\Delta ) = \frac{{\left| {2.( - 2) - 3.1 + 5} \right|}}{{\sqrt {{2^2} + {{( - 3)}^2}} }} = \frac{2}{{\sqrt {13} }} = \frac{{2\sqrt {13} }}{{13}}\). b) Đường thẳng \(\Delta \) đi qua điểm N(-2;2) và có vecto pháp tuyến \(\overrightarrow n = (4;3)\). Phương trình đường thẳng \(\Delta \) là \(4(x + 2) + 3(y - 2) = 0\). Từ đó, ta nhận được phương trình tổng quát của đường thẳng \(\Delta \) là \(4x + 3y + 2 = 0\). Vậy \(d(M,\Delta ) = \frac{{\left| {4.1 + 3.( - 3) + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} = \frac{3}{5}\).
HocTot.XYZ
|