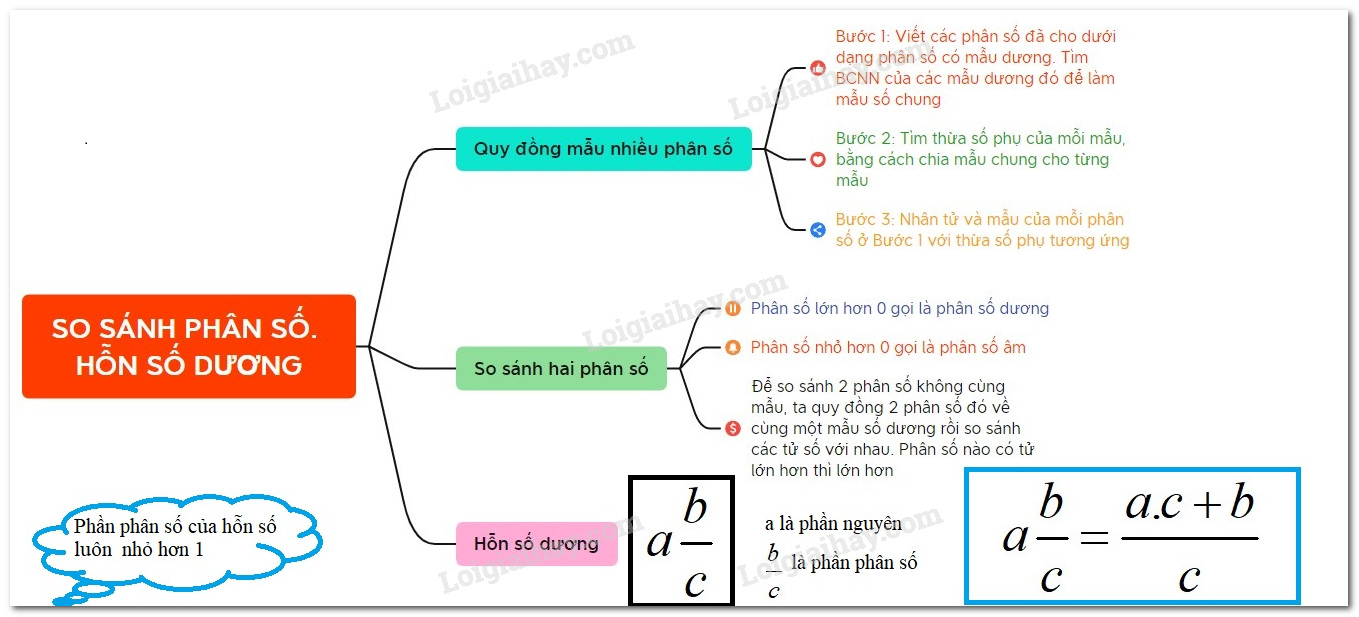
Lý thuyết So sánh phân số. Hỗn số dương Toán 6 KNTT với cuộc sốngLý thuyết So sánh phân số. Hỗn số dương Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu Phân số dương. Hỗn số dương 1. Quy đồng mẫu số nhiều phân số Để quy đồng nhiều phân số, ta thường làm như sau: Bước 1: Viết các phân số đã cho dưới dạng phân số có mẫu dương. Tìm BCNN của các mẫu dương đó để làm mẫu số chung Bước 2: Tìm thừa số phụ của mỗi mẫu, bằng cách chia mẫu chung cho từng mẫu Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng Ví dụ: Để quy đồng mẫu hai phân số $\dfrac{1}{6}$ và $\dfrac{3}{{ - 8}}$, ta làm như sau: - Đưa về phân số có mẫu dương: $\dfrac{1}{6}$ và $\dfrac{{ - 3}}{8}$ - Tìm mẫu chung: $BC(6,\,8) = 24$ - Tìm thừa số phụ: $24:6 = 4;\,24:8 = 3$ - Ta có: $\dfrac{1}{6} = \dfrac{{1.4}}{{6.4}} = \dfrac{4}{{24}}$ và $\dfrac{3}{{ - 8}} = \dfrac{{ - 3}}{8} = \dfrac{{ - 3.3}}{{8.3}} = \dfrac{{ - 9}}{{24}}$. 2. Rút gọn phân sốa) Khái niệm phân số tối giản: Phân số tối giản là phân số mà tử và mẫu chỉ có ước chung là $1$ và $ - 1$ b) Cách rút gọn phân số Bước 1: Tìm ƯCLN của tử và mẫu khi đã bỏ dấu “-” (nếu có) Bước 2: Chia cả tử và mẫu cho ƯCLN vừa tìm được, ta có phân số tối giản. Ví dụ: Để rút gọn phân số $\dfrac{{ - 15}}{{24}}$ ta làm như sau: - Tìm ƯCLN của mẫu: ƯCLN(15, 24)=3. - Chia cả tử và mẫu cho ƯCLN: $\dfrac{{ - 15}}{{24}} = \dfrac{{ - 15:3}}{{24:3}} = \dfrac{{ - 5}}{8}$. Ta được $\dfrac{{ - 5}}{8}$ là phân số tối giản. 3. So sánh hai phân số cùng mẫuTrong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn. Ví dụ: So sánh $\dfrac{{ - 4}}{5}$ và $\dfrac{{ - 7}}{5}$. Ta có: $ - 4 > - 7$ và $5 > 0$ nên $\dfrac{{ - 4}}{5} > \dfrac{{ - 7}}{5}$. Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh. Ví dụ: So sánh $\dfrac{{ - 4}}{{ - 5}}$ và $\dfrac{2}{{ - 5}}$ Đưa hai phân số trên về có cùng một mẫu nguyên âm: $\dfrac{4}{5}$ và $\dfrac{{ - 2}}{5}$ Ta có: $4 > - 2$ và $5 > 0$ nên $\dfrac{4}{5} > \dfrac{{ - 2}}{5}$. 4. So sánh hai phân số khác mẫuBước 1: Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương) Bước 2: So sánh tử của các phân số: Phân số nào có tử lớn hơn thì lớn hơn. Ví dụ: So sánh hai phân số $\dfrac{{ - 7}}{{12}}$ và $\dfrac{{ - 11}}{{18}}$. $BCNN(12;18) = 36$ nên ta có: $\dfrac{{ - 7}}{{12}} = \dfrac{{ - 7.3}}{{12.3}} = \dfrac{{ - 21}}{{36}}$ $\dfrac{{ - 11}}{{18}} = \dfrac{{ - 11.2}}{{18.2}} = \dfrac{{ - 22}}{{36}}$. Vì $ - 21 > - 22$ nên $\dfrac{{ - 21}}{{36}} > \dfrac{{ - 22}}{{36}}$. Do đó $\dfrac{{ - 7}}{{12}} > \dfrac{{ - 11}}{{18}}$. 5. Hỗn sốCho $a$ và $b$ là hai số nguyên dương, $a > b$, $a$ không chia hết cho $b$. Nếu $a$ chia cho $b$ được thương là $q$ và số dư là $r$, thì ta viết $\dfrac{a}{b} = q\dfrac{r}{b}$ và gọi $q\dfrac{r}{b}$ là hỗn số. Đọc là “$q,\,\,r$ phần $b$”. Ví dụ: Phép chia $23:4$ có thương là $5$ và số dư là $3$ nên ta có: $\dfrac{{23}}{4} = 5\dfrac{3}{4}$. Đọc là: “ năm, ba phần tư”. Chú ý: Với hỗn số $q\dfrac{r}{b}$ người ta gọi $q$ là phần số nguyên và $\dfrac{r}{b}$ là phần phân số của hỗn số. Ví dụ: Hỗn số $5\dfrac{3}{4}$ có phần nguyên là $5$ và phần phân số là $\dfrac{3}{4}$. * Đổi hỗn số ra phân sốTa đổi hỗn số $q\dfrac{r}{b}$ thành phân số, theo quy tắc sau: $q\dfrac{r}{b} = \dfrac{{q.b + r}}{b}$ Ví dụ: $1\dfrac{3}{4} = \dfrac{{1.4 + 3}}{4} = \dfrac{7}{4}$
|