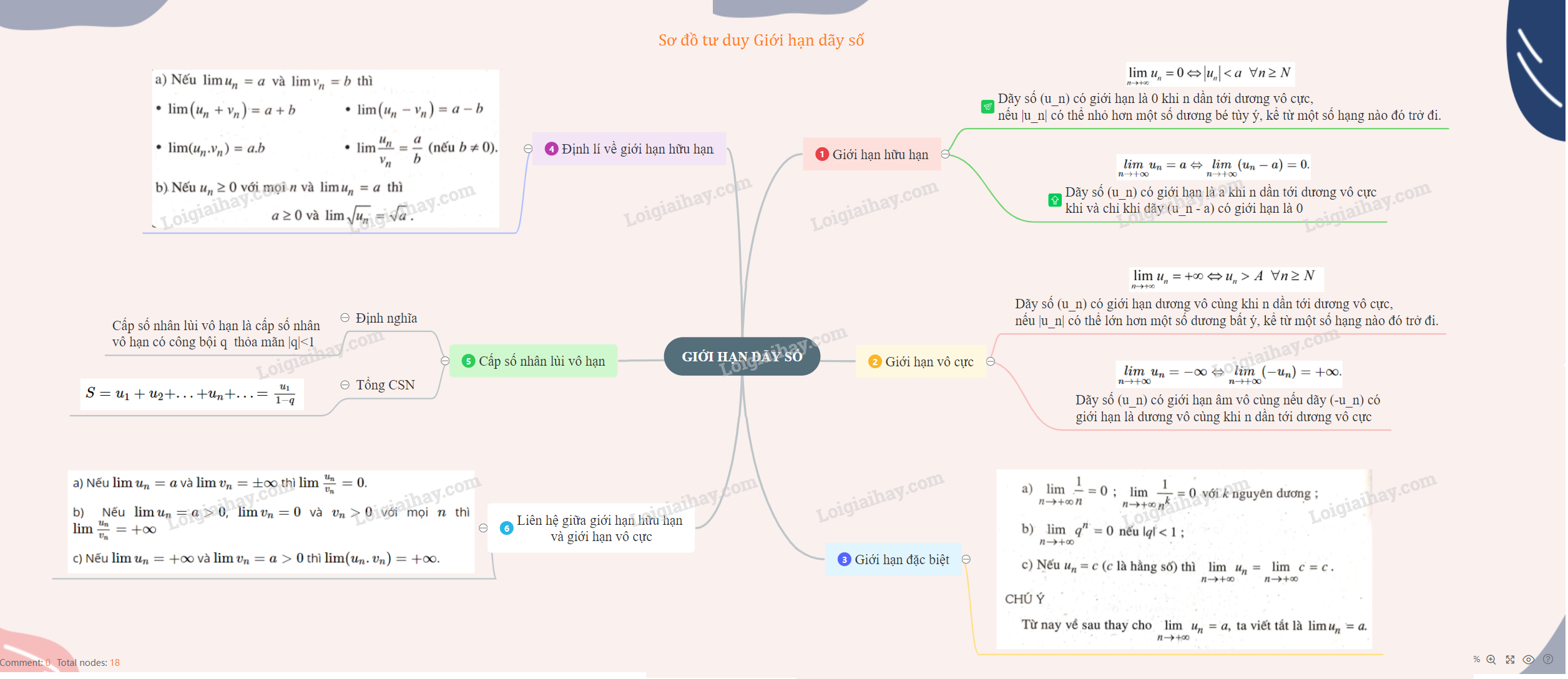
Lý thuyết về giới hạn của dãy số

A. LÝ THUYẾT

1. Giới hạn hữu hạn

+) \(\underset{n\rightarrow +\infty }{\lim }u_{n} = 0\) khi và chỉ khi \(|u_n|\) có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.

+) \(\underset{n\rightarrow +\infty }{\lim }u_{n} = a \Leftrightarrow \underset{n\rightarrow +\infty }{\lim }(u_{n}-a) = 0\).

2. Giới hạn vô cực

+) \(\underset{n\rightarrow +\infty }{\lim }u_{n}= +∞\) khi và chỉ khi \(u_n\) có thể lớn hơn một số dương tùy ý, kể từ một số hạng nào đó trở đi.

+) \(\underset{n\rightarrow +\infty }{\lim }u_{n} = -∞ \Leftrightarrow \underset{n\rightarrow +\infty }{\lim}(-u_{n})= +∞\).

3. Các giới hạn đặc biệt

a) \(\lim \frac{1}{n} = 0\);

\(\lim \frac{1}{n^{k}} = 0\);

\(\lim n^k= +∞\), với \(k\) nguyên dương.

b) \(\lim q^n= 0\) nếu \(|q| < 1\);

\(\lim q^n= +∞\) nếu \(q > 1\).

c) \(\lim c = c\) (\(c\) là hằng số).

4. Định lí về giới hạn hữu hạn

a) Nếu \(\lim u_n=a\) và \(\lim v_n= b\), thì:

\(\lim\left( {{u_{n}}+{v_n}} \right)= a +b\)

\(\lim({u_n} - {v_n}){\rm{ }} = {\rm{ }}a - b\)

\(\lim({u_n}.{v_n}) = ab\)

\(\lim{{{u_n}} \over {{v_n}}} = {a \over b}\) (nếu \(b ≠ 0\)).

b) Nếu \(u_n≥ 0\) với mọi \(n\) và \(\lim u_n= a\) thì \(a > 0\) và \(\lim \sqrt{u_n}= \sqrt a\).

5. Định lí liên hệ giữa giới hạn hữu hạn và giới hạn vô cực.

a) Nếu \(\lim u_n=a\) và \(\lim v_n= ± \infty\) thì \(\lim \frac{u_{n}}{v_{n}}= 0\).

b)  Nếu \(\lim u_n=a > 0\), \(\lim v_n= 0\) và \(v_n> 0\) với mọi \(n\) thì \(\lim \frac{u_{n}}{v_{n}} = +\infty\).

c) Nếu \(\lim u_n= +\infty\) và \(\lim v_n= a > 0\) thì \(\lim (u_n.v_n) = +\infty\).

6. Cấp số nhân lùi vô hạn

+ Cấp số nhân lùi vô hạn là cấp số nhân vô hạn có công bội \(q\) thỏa mãn \(|q| <1\).

+) Công thức tính tổng \(S\) của cấp số lùi vô hạn \((u_n)\):

\(S = {u_1} + {u_2} + ... + {u_n} + ... = {{{u_1}} \over {1 - q}}\).

B. BÀI TẬP

Bài 1. Cho dãy số $(u_{n})$ có tính chất $|u_{n}-2|\leq\frac{1}{3^{n}}$. Tính $\lim_{n\to+\infty}u_{n}$.

Giải:

Do $\lim_{n\to+\infty}\frac{1}{3^{n}}=0$ nên $\lim_{n\to+\infty}(u_{n}-2)=0$.

Vậy $\lim_{n\to+\infty}u_{n}=2$.

Bài 2. Tính $\lim_{n\to+\infty}\frac{2n^{2}+1}{3n^{2}+n}$.

Giải:

$\lim_{n\to+\infty}\frac{2n^{2}+1}{3n^{2}+n}=\lim_{n\to+\infty}\frac{2+\frac{1}{n^{2}}}{3+\frac{1}{n}}=\frac{2}{3}$.

Bài 3. Tính $\lim_{n\to+\infty}(\sqrt{n^{2}-n}-\sqrt{n^{2}+1})$.

Giải:

$\lim_{n\to+\infty}(\sqrt{n^{2}-n}-\sqrt{n^{2}+1})$

$=\lim_{n\to+\infty}\frac{-n-1}{\sqrt{n^{2}-n}+\sqrt{n^{2}+1}}$

$=\lim_{n\to+\infty}\frac{-1-\frac{1}{n}}{\sqrt{1-\frac{1}{n}}+\sqrt{1+\frac{1}{n^{2}}}}=-\frac{1}{2}$.

Bài 4. Tính $\lim_{n\to+\infty}(n^{2}-n+3)$.

Giải:

$\lim_{n\to+\infty}(n^{2}-n+3)$

$=\lim_{n\to+\infty}n^{2}\left(1-\frac{1}{n}+\frac{3}{n^{2}}\right)=+\infty$.

Bài 5. Tính tổng $S=\frac{1}{3}+\frac{1}{9}-\frac{1}{27}+\cdots+(-1)^{n}\frac{1}{3^{n}}+\cdots$

Giải:

Ta thấy $S$ là tổng của cấp số nhân lùi vô hạn $(u_{n})$ với $u_{1}=-\frac{1}{3},q=-\frac{1}{3}.$

Do đó $S=\frac{u_{1}}{1-q}=\frac{-\frac{1}{3}}{1+\frac{1}{3}}=-\frac{1}{4}$.

HocTot.XYZ