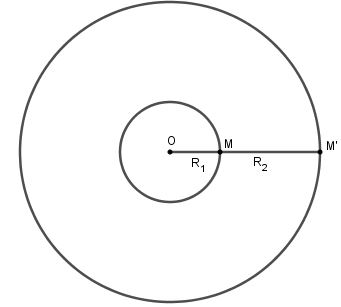
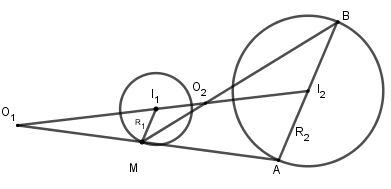
Câu hỏi 6 trang 34 SGK Hình học 11Nêu cách tìm tâm vị tự của hai đường tròn. Đề bài Nêu cách tìm tâm vị tự của hai đường tròn. Lời giải chi tiết Gọi hai đường tròn là \(({I_1}{\rm{; }}{R_1})\) và \(({I_2}{\rm{; }}{R_2})\). + TH1: \({I_1}\; \equiv {\rm{ }}{I_2}\) Khi đó tâm vị tự \(O \equiv {\rm{ }}{I_1}\; \equiv {\rm{ }}{I_2}\); tỉ số vị tự \({k_1} = \frac{{{R_2}}}{{{R_1}}}\) và \({k_2} = - \frac{{{R_2}}}{{{R_1}}}\) biến đường tròn \(({I_1}{\rm{; }}{R_1})\) thành đường tròn \(({I_2}{\rm{; }}{R_2})\). + TH2: \({I_1}\; \ne {\rm{ }}{I_2}.\) Vẽ bán kính \(I_1 M\) bất kì. Dựng đường kính \(AB\) của \(({I_2}{\rm{; }}{R_2})\) sao cho \(AB // I_1M.\) \(MA; MB\) lần lượt cắt \(I_1 I_2\) tại \(O_1\) và \(O_2\). Khi đó \(O_1\) và \(O_2\) chính là hai tâm vị tự của hai đường tròn. HocTot.XYZ
|