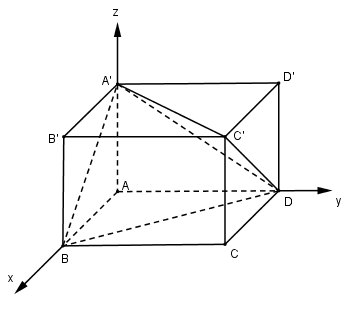
Bài 12 trang 124 SGK Hình học 12 Nâng caoCho hình hộp chữ nhật ABCD.A’B’C’D’ với AB = a, BC = b, CC’ = c. a) Tính khoảng cách từ điểm A tới mp(A’BD). b) Tính khoảng cách từ điểm A’ tới đường thẳng C’D. c) Tính khoảng cách giữa hai đường thẳng BC’ và CD’.
Lựa chọn câu để xem lời giải nhanh hơn
Cho hình hộp chữ nhật ABCD.A’B’C’D’ với AB = a, BC = b, CC’ = c. LG a Tính khoảng cách từ điểm A tới mp(A’BD). Lời giải chi tiết: Chọn hệ trục tọa độ Oxyz như hình vẽ.
Ta có: \(A'\left( {0;0;c} \right),\,\,B\left( {a;0;0} \right),\,\,D\left( {0;b;0} \right).\) \(d = {{\left| { - 1} \right|} \over {\sqrt {{1 \over {{a^2}}} + {1 \over {{b^2}}} + {1 \over {{c^2}}}} }} = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}.\) LG b Tính khoảng cách từ điểm A’ tới đường thẳng C’D. Lời giải chi tiết: Ta có \(C'\left( {a;b;c} \right).\) \(\eqalign{ Khoảng cách từ \(A'\left( {0,0,c} \right)\) tới đường thẳng C’D là: \({h_1} = {{\left| {\left[ {\overrightarrow {A'C'} ,\overrightarrow {C'D} } \right]} \right|} \over {\left| {\overrightarrow {C'D} } \right|}} = {{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} } \over {\sqrt {{a^2} + {c^2}} }}.\) LG c Tính khoảng cách giữa hai đường thẳng BC’ và CD’. Lời giải chi tiết: Ta có \(\overrightarrow {BC'} = \left( {0,b,c} \right),\overrightarrow {CD'} = \left( { - a,0,c} \right),\) \(\overrightarrow {BC} = \left( {0,b,0} \right).\) Khoảng cách giữa BC’ và CD’ là: \({h_2} = {{\left| {\left[ {\overrightarrow {BC'} ,\overrightarrow {CD'} } \right].\overrightarrow {BC} } \right|} \over {\left| {\left[ {\overrightarrow {BC'} ,\overrightarrow {CD'} } \right]} \right|}} = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}.\) HocTot.XYZ
|