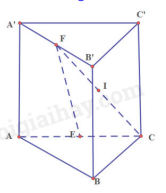
Bài 3 trang 113 SGK Toán 11 tập 1 - Cánh DiềuCho hình lăng trụ tam giác ABC.A’B’C‘. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B‘. Đề bài Cho hình lăng trụ tam giác ABC.A’B’C'. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B‘. a) Chứng minh rằng EF // (BCC’B’). b) Gọi I là giao điểm của đường thẳng CF với mặt phẳng (AC’B). Chứng minh rằng I là trung điểm đoạn thẳng CF. Phương pháp giải - Xem chi tiết Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với (P). Lời giải chi tiết
a) Gọi H là trung điểm của BC Tam giác ABC có: E là trung điểm của AC Suy ra EH // AB Mà AB // A’B’ Do đó EH // A’B’ hay EH // B’F (1) Ta có: EH // AB nên Mà AB = A’B'', Nên EH = B’F (2) Từ (1) và (2) suy ra: EHB’F là hình bình hành Suy ra EF // B’H Suy ra EF // (BCC’B’) b) Gọi K là trung điểm AB Dễ dàng chứng minh FKBB’ là hình bình hành Ta có: FK // BB' Mà BB' // CC' Suy ra FK // CC' (1) Ta có: FK = BB', mà BB' = CC' Do đó: FK = CC' (2) Từ (1) và (2) suy ra FKCC’ là hình bình hành Suy ra C’K cắt CF tại trung điểm mỗi đường Suy ra I là trung điểm của CF
|