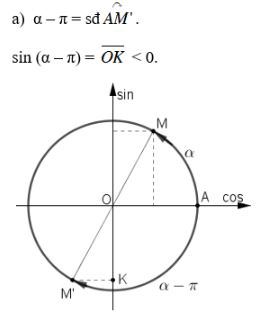
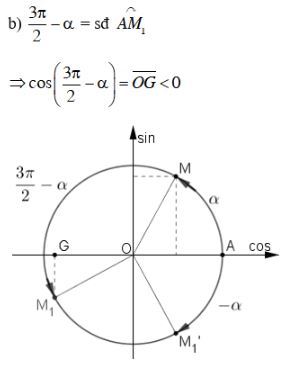
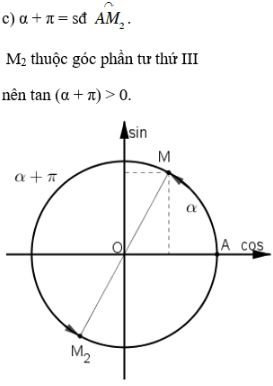
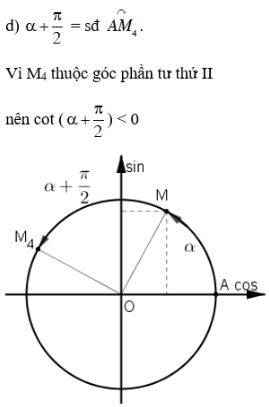
Bài 3 trang 148 SGK Đại số 10Cho 0 < α < . Xác định dấu của các giá trị lượng giác < π/2. Video hướng dẫn giải Cho \(0 < α < \frac{\pi }{2}\). Xác định dấu của các giá trị lượng giác LG a \(\sin(α - π)\); Phương pháp giải: Áp dụng các công thức đặc biệt: \(\sin \left( {\pi - x } \right) = \sin x \) và \(\sin \left( { - x } \right) = - \sin x \) Lời giải chi tiết: Với \(0 < α < \dfrac{\pi}{2}\) ta có: \(\sin \alpha > 0,\cos \alpha > 0,\) \(\tan\alpha > 0,\cot \alpha > 0.\) \(\sin \left( {\alpha - \pi } \right)\) \( = \sin \left[ { - \left( {\pi - \alpha } \right)} \right]\) \( = - \sin \left( {\pi - \alpha } \right) \) (áp dụng \(\sin \left( { - x } \right) = - \sin x \) với \(x = \pi - \alpha \)) \(= - \sin \alpha \) (áp dụng \(\sin \left( {\pi - x } \right) = \sin x \) với \(x=\alpha\)) Mà \(\sin \alpha > 0\) nên \( - \sin \alpha < 0\) hay \(\sin \left( {\alpha - \pi } \right) < 0\). Cách khác LG b \(\cos\left( \dfrac{3\pi }{2}- α\right)\) Phương pháp giải: Áp dung các công thức đặc biệt: \(\cos \left( {\pi + \alpha } \right) = - \cos \alpha \) và \(\cos \left( {\dfrac{\pi }{2} - \alpha } \right) = \sin \alpha \) Lời giải chi tiết: Ta có: \(\cos \left( {\dfrac{{3\pi }}{2} - \alpha } \right) \) \(= \cos \left( {\pi + \dfrac{\pi }{2} - \alpha } \right) \) \(= - \cos \left( {\dfrac{\pi }{2} - \alpha } \right) \) (áp dụng \(\cos \left( {\pi + x} \right) = - \cos x\) với \(x = \frac{\pi }{2} - \alpha \)) \(= - \sin\alpha .\) (áp dụng \(\cos \left( {\frac{\pi }{2} - x} \right) = \sin x\) với \(x=\alpha \)) Mà \(\sin\alpha >0\) nên \(- \sin\alpha <0\) hay \(\cos \left( {\dfrac{{3\pi }}{2} - \alpha } \right) <0\). Cách khác: LG c \(\tan(α + π)\); Phương pháp giải: Áp dụng công thức đặc biệt: \(\tan \left( {\alpha + \pi } \right) = \tan \alpha\) Lời giải chi tiết: Ta có: \(\tan \left( {\alpha + \pi } \right) = \tan \alpha .\) Mà \(\tan α > 0\) nên \(\tan (α + π) > 0\). Cách khác: LG d \(\cot\left(α + \dfrac{\pi }{2}\right)\) Phương pháp giải: Áp dụng các công thức đặc biệt: \(\cot \left( {\dfrac{\pi }{2} - \alpha } \right) = \tan \alpha \) và \(\tan \left( { - \alpha } \right) = - \tan \alpha \) Lời giải chi tiết: \(\cot \left( {\dfrac{\pi }{2} + \alpha } \right) = \cot \left[ {\dfrac{\pi }{2} - \left( { - \alpha } \right)} \right]\) \( = \tan \left( { - \alpha } \right) = - \tan \alpha \) Mà \(\tan \alpha > 0\) nên \( - \tan \alpha < 0\) hay \(\cot \left( {\dfrac{\pi }{2} + \alpha } \right) < 0\). Cách khác: HocTot.XYZ
|