Bài 3 trang 63 SGK Hình học 12 Nâng caoCho hai đường tròn (O; r) và (O’; r’) cắt nhau tại hai điểm A, B và lần lượt nằm trên hai mặt phẳng phân biệt (P) và (P’). Đề bài Cho hai đường tròn \((O; r)\) và \((O’; r’)\) cắt nhau tại hai điểm \(A, B\) và lần lượt nằm trên hai mặt phẳng phân biệt \((P)\) và \((P’)\). a) Chứng minh rằng có mặt cầu \((S)\) đi qua hai đường tròn đó. b) Tìm bán kính \(R\) của mặt cầu \((S)\) khi \(r = 5, r' = \sqrt {10} \), \(AB = 6\), \({\rm{OO}}' = \sqrt {21} \). Lời giải chi tiết
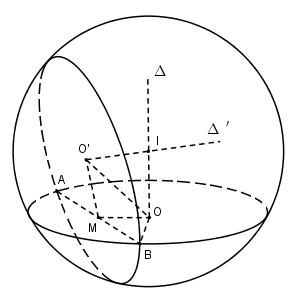
Gọi \(\Delta ,\,\Delta '\) lần lượt là trục của đường tròn \((O; r)\) và \((O’; r’)\) thì \(AB \bot \Delta \,\,,\,\,AB \bot \Delta '\). Do đó \(\Delta ,\,\Delta '\) cùng nằm trong mp \((OO’M)\). Gọi \(I\) là giao điểm của \(\Delta \) và \(\Delta '\) thì \(I\) là tâm của mặt cầu \((S)\) đi qua hai đường tròn \((O; r)\) và \((O’; r’)\) và \(S\) có bán kính \(R = IA\). b) Ta có: \(MA = MB = 3\,\,,\,\,OA = r = 5,\,\,OA' = r' = \sqrt {10} \) \(\eqalign{ Áp dụng định lí Cosin trong \(\Delta {\rm{OMO'}}\) ta có: \(\eqalign{ Áp dụng định lí Côsin trong tam giác \(OMO’\) ta có: \(\eqalign{ (Vì \(\widehat {MO'O} + \widehat {OO'I} = {90^0}\)) Áp dụng định lí Cosin trong tam giác \(OIO’\) ta có: Vậy \(R = \sqrt {O{A^2} + O{I^2}} = \sqrt {25 + 12} = \sqrt {37} \) HocTot.XYZ
|