Bài 6 trang 63 Hình học 12 Nâng caoMột hình thang cân ABCD có các cạnh đáy AB = 2a, BD = 4a, cạnh bên AD = BC = 3a. Hãy tính thể tích và diện tích toàn phần của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó. Đề bài Một hình thang cân \(ABCD\) có các cạnh đáy \(AB = 2a, BD = 4a\), cạnh bên \(AD = BC = 3a\). Hãy tính thể tích và diện tích toàn phần của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó. Lời giải chi tiết
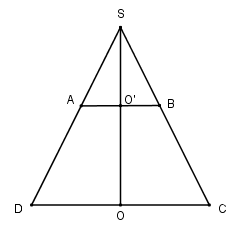
Gọi \(S\) là giao điểm của hai cạnh bên \(AD\) và \(BC\) của hình thang. Đường cao \(SO\) của tam giác cân \(SCD\) là trục đối xứng của hình thang, do đó \(SO\) cắt \(AB\) tại trung điểm \(O’\) của \(AB\). Khi quay quanh \(SO\), tam giác \(SCD\) sinh ra khối nón \(\left( {{N_1}} \right)\) có thể tích \({V_1}\), tam giác \(SAB\) sinh ra khối nón \(\left( {{N_2}} \right)\) có thể tích \({V_2}\), còn hình thang \(ABCD\) sinh ra một khối tròn xoay \(\left( H \right)\) có thể tích \(V = {V_1} - {V_2}\). Vì \(AB = {1 \over 2}CD\) nên \(AB\) là đường trung bình của tam giác \(SCD\) nên \(SB = BC = 3a\). Ta có \(SO' = \sqrt {S{B^2} - O'{B^2}} \) \( = \sqrt {9{a^2} - {a^2}} = 2\sqrt 2 a\) \(\eqalign{ Diện tích xung quanh của khối tròn xoay \((H)\) là: \(\eqalign{ HocTot.XYZ
|