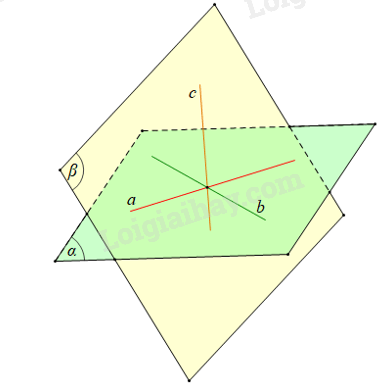
Bài 3 trang 94 SGK Toán 11 tập 1 - Cánh diềuCho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy. Đề bài Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy. Phương pháp giải - Xem chi tiết Chứng minh giao điểm của ba đường thẳng nằm trên cùng một mặt phẳng, khi đó a, b, c cùng thuộc một mặt phẳng (trái với giả thiết) => giao điểm của ba đường thẳng phải trùng nhau. Lời giải chi tiết
Giả sử a ∩ b = {I} và α = mp(a, b); a ∩ c = {J} và β = mp(a, c); b ∩ c = {K} và γ = mp(b, c) với các điểm I, J, K phân biệt. Khi đó α ∩ β = a và đường thẳng a chính là đường thẳng IJ. α ∩ γ = b và đường thẳng b chính là đường thẳng IK. β ∩ γ = c và đường thẳng c chính là đường thẳng JK. Mà chỉ có một mặt phẳng duy nhất đi qua ba điểm I, J, K, đó là (IJK) Khi đó a, b, c cùng thuộc mặt phẳng (IJK), điều này trái với giả thiết a, b, c không cùng nằm trong một mặt phẳng. Vậy I, J, K phải trùng nhau hay a, b, c đồng quy.
|