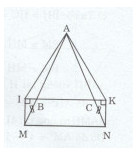
Bài 4 trang 175 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác ABC cân tại A. Trên tia đối của tia BA lây điểm M, trên tia đối của tia CA lấy điểm N sao cho MB = NC. Kẻ $MI \bot BC(I \in BC)$  và $NK \bot BC(K \in BC).$  Chứng minh rằng :

a) $\Delta MBI = \Delta NCK.$

b) $\Delta AIK$ cân.

c) IK // MN.

Lời giải chi tiết

 

a)Ta có: $\eqalign{  & \widehat {ABC} = \widehat {IBM}  \cr  & \widehat {ACB} = \widehat {KCN} \cr}$  (hai góc đối đỉnh)

Mà $\widehat {ABC} = \widehat {ACB}(\Delta ABC$ cân tại A) nên $\widehat {IBM} = \widehat {KCN.}$

Xét tam giác MBI vuông tại I và tam giác NCK vuông tại K ta có:

$\eqalign{  & \widehat {IBM} = \widehat {KCN}(cmt)  \cr  & MB = NC(gt) \cr}$

Do đó: $\Delta MBI = \Delta NCK$  (cạnh huyền - góc nhọn)

b) Ta có: AB = AC (tam giác ABC cân tại A) và BM = CN (giả thiết)

=>AB + BM = AC + CN => AM = AN.

Xét tam giác AIM và AKN ta có:

$\eqalign{  & IM = KN(\Delta MBI = \Delta NCK)  \cr  & \widehat {IMA} = \widehat {KNA}(\Delta MBI = \Delta NCK) \cr}$

Do đó: $\Delta AIM = \Delta AKN(c.g.c) \Rightarrow AI = AK.$   Vậy tam giác AIK cân tại A.

c) Tam giác ABC cân tại A $\Rightarrow \widehat {ABC} = \widehat {ACB}.$  Do đó: $\widehat {ABC} = {{{{180}^0} - \widehat {BAC}} \over 2}(1)$

Mặt khác AM = AN => tam giác AMN cân tại A $\Rightarrow \widehat {AMN} = \widehat {ANM}.$

Do đó: $\widehat {AMN} = {{{{180}^0} - \widehat {BAC}} \over 2}(2)$

Từ (1) và (2) ta có: $\widehat {ABC} = \widehat {AMN}.$

Mà hai góc ABC và AMN đồng vị. Vậy IK // MN.

HocTot.XYZ