Bài 4 trang 45 SGK Hình học 12 Nâng caoCho đường thẳng d và điểm A không nằm trên d. Xét các mặt cầu đi qua A và có tâm nằm trên d. Chứng minh rằng các mặt cầu đó luôn đi qua một đường tròn cố định. Đề bài Cho đường thẳng \(d\) và điểm \(A\) không nằm trên \(d\). Xét các mặt cầu đi qua \(A\) và có tâm nằm trên \(d\). Chứng minh rằng các mặt cầu đó luôn đi qua một đường tròn cố định. Lời giải chi tiết
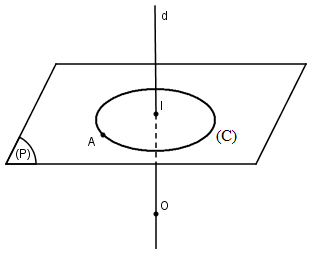
Giả sử \((S)\) là một mặt cầu đi qua \(A\) và có tâm \(O\) nằm trên \(d\). Gọi \((P)\) là mặt phẳng đi qua \(A\) và vuông góc với \(d\), \((P)\) cắt mặt cầu \((S)\) theo đường tròn \((C)\) có tâm là giao điểm \(I\) của \((P)\) và \(d\), có bán kính \(r = IA\). Vậy đường tròn \((C)\) cố định và mặt cầu \((S)\) luôn luôn đi qua \((C)\). HocTot.XYZ
|