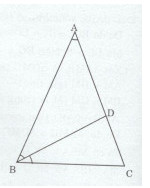
Bài 5 trang 171 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác ABC cân tại A có $\widehat B = 2\widehat A.$  Phân giác của góc B cắt AC tại D.

a) Tính số đo các góc của tam giác ABC.

b) Chứng minh rằng DA = DB.

c) Chứng minh rằng DA = BC.

Lời giải chi tiết

 

a)Ta có:

$\widehat {ABC} = \widehat {ACB}(\Delta ABC$  cân tại A)

$\widehat {ABC} = 2\widehat {BAC}(gt)$

Nên $\widehat {ACB} = 2\widehat {BAC}$

Mà tam giác ABC có: $\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^0}.$

Do đó: $\eqalign{  & \widehat {BAC} + 2\widehat {BAC} + 2\widehat {BAC} = {180^0}  \cr  &  \Rightarrow 5\widehat {BAC} = {180^0} \Rightarrow \widehat {BAC} = {{{{180}^0}} \over 5} = {36^0} \cr}$

Do đó: $\widehat {ABC} = \widehat {ACB} = {2.36^0} = {72^0}.$

b) Ta có: $\widehat {BAD} = {{\widehat {ABC}} \over 2}(gt)$

$\widehat {ABD} = \widehat {DBC} = {{\widehat {ABC}} \over 2}$   (BD là tia phân giác của ABC)

Do đó: $\widehat {BAD} = \widehat {ABD} = \widehat {DBC}.$

Tam giác ADB có: $\widehat {DAB} = \widehat {ABD} \Rightarrow \Delta ADB$  cân tại D.

Vậy DA = DB.

c) Ta có: $\widehat {BDC} = \widehat {ABD} + \widehat {DAB}$   (góc ngoài của tam giác ABD)

Mà $\widehat {ABD} = \widehat {DAB}$   nên $\widehat {BDC} = 2\widehat {BAD}$

$\widehat {ABC} = \widehat {ACB} = 2\widehat {BAD}(\Delta ABC$  cân tại A và $\widehat B = 2\widehat A)$

Suy ra: $\widehat {BDC} = \widehat {DCB} \Rightarrow \Delta BDC$  cân tại B => BD = BC.

Mà AD = BD (chứng minh trên). Do đó: BC = AD.

HocTot.XYZ